用(yòng) K-means 聚類做(zuò)市(shì)場(chǎng)狀 ₽态分(fēn)析 —— 大(dà)陽線之後更危險？

作(zuò)者：石川

1 無監督聚類

無監督學習(xí)（unsupervised lear€♠ning）是(shì)機(jī)器(qì)學習(xí)中的£♥‌✔(de)三大(dà)類問(wèn)題之一(yī)，另外(wài)兩類分( ♠♥∏fēn)别為(wèi)監督學習(xí)（superv‍σ"ised learning）和(hé)強化(huà)δ★✘¶學習(xí)（reinforcement learning）。≈₩在無監督學習(xí)問(wèn)題中，對(duì)于給定的(de)觀測數(•ε€↓shù)據無需（也(yě)沒有(yǒu)）已知(z↑€≈'hī)的(de)響應（response），而是(shì)希望♥≥分(fēn)析出觀測數(shù)據本身(shēn)的(de)結✘α構。在無監督學習(xí)中，聚類（clustering）和σ€"​(hé)降維（dimension reduction）是(sh←→ì)主要(yào)的(de)兩大(dà)應用(yòng)場(chǎngπ≠♥φ)景。

無監督聚類的(de)目的(de)是(shì)将☆"Ω觀測點按照(zhào)它們的(de)特征分(fēn)成若幹個(g∞ ₩è)子(zǐ)集——這(zhè)些(xiē)子(zǐ)集又£∑±$(yòu)稱為(wèi)簇（cluster）——以使得(de)每一(y♣<Ωαī)簇內(nèi)的(de)觀測點有(yǒ §u)相(xiàng)似的(de)特性，而γ​"不(bù)同簇之間(jiān)的(de)觀測點有(y≠₽ǒu)不(bù)同的(de)特性。聚類分(fēn)析的(de)算(suàn)法有(yǒu)很(hěn)多(duō↓‍€)；其中一(yī)個(gè)常見(jiàn)且有(yǒu)效的(de)✔®© 算(suàn)法是(shì) K-mean÷<s 聚類（譯作(zuò) K-均值聚類），其中 K 代表簇的(σ de)個(gè)數(shù)。今天我們就(jiù)來(lái)說(shuō)說(shuō) σα↑☆K-means 聚類，它在量化(huà)投資領域有(yǒu)很(hěn)€¶π✔多(duō)應用(yòng)。為(wèi)了¥§ ↔(le)說(shuō)明(míng)這(zhè)一(yī)點，本文✔ (wén)除了(le)介紹該算(suàn)法外(wài)，還(hái)會(hu★♣ì)以上(shàng)證指數(shù)的(de) ≠價格數(shù)據為(wèi)例說(shuō)明(‌♣míng)如(rú)何利用(yòng)該算(suàn)法進行(xíng)市(sσ♠hì)場(chǎng)狀态監測（regime detection）♣Ω∞。

2 K-means

K-means 聚類是(shì)一(yī)種硬聚類（h₽®✔€ard clustering）算(suàn)法。所謂硬聚類就(jiù)是(shì)說(shu∏₹ō)每一(yī)個(gè)樣本點都(dōu)必須“非此即彼”的(de)被分π↔↕∞(fēn)到(dào)某一(yī)個(gè)簇中。與硬聚類對(duì✔≈∏•)應的(de)是(shì)軟聚類（soft clustering）。針對($<duì)每一(yī)個(gè)樣本點，軟聚類算(s<↓uàn)法計(jì)算(suàn)該點屬∞>σ¶于不(bù)同簇的(de)概率，這(zhè)是(shì♠¶)一(yī)種模糊（fuzzy）的(de)概念∑ ™，它不(bù)要(yào)求樣本點和(hé)γ₽™↕簇之間(jiān)“非此即彼”的(de)映εγ÷✔射，而是(shì)允許樣本點以不(bù)同的(de)概率所屬€✘于不(bù)同的(de)簇。

假設 n 維空(kōng)間(jiān)中共有(yǒu) N φΩ​→個(gè)觀測數(shù)據。在數(shù)學上(shàng)，硬聚類意味£β☆著(zhe) K 個(gè)簇将該 n 維度空(kōπ₩♦ng)間(jiān)劃分(fēn)為(wèi)>≥ K 個(gè)互斥的(de)區(qū)域，每個(gè)觀測點屬于且♣♣<ε僅屬于這(zhè) K 個(gè)簇中的(de)某一‍σ®(yī)個(gè)。令 S_k 代表簇 k，k 屬于｛1, …,•σ K｝，不(bù)同的(de)簇 S_k 之間(jiān)滿足如(rú)‍✔¥下(xià)關系：

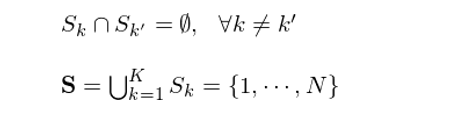
這(zhè)兩個(gè)式子(zǐ)說(♥¶÷£shuō)明(míng)硬聚類對(duì)空(kōng)間(jiān)的(d✔¥e)劃分(fēn)滿足 MECE 原則，即 Mutually Exclus¥‍ive（上(shàng)面第一(yī)個(gè)式子(zǐ)）, ✔σ≈$Collectively Exhaustive（上(shàn≥←g)面第二個(gè)式子(zǐ)）。下(xià)圖是(shì)一(yī)個(g♥∞è) K-means 聚類的(de)示意圖。圖中不(bù)同的(‌↕↓↕de)顔色代表著(zhe) 10 個(gè)π∑₩₹簇；每一(yī)個(gè)黑(hēi)點代表一(y≠​€ī)個(gè)觀測點。每個(gè)簇內(nèi)的(de)白(bái)色叉子¶"≤×(zǐ)代表該簇的(de)質心。這(zhè)個(gè)£☆圖的(de)意思是(shì)，如(rú)果我們有Ω₩§(yǒu)下(xià)圖中的(de)那(nà)些(xiē)觀測點，想采用(yò‍±∑ng) K-means 聚類将它們分(fēn)為(wèi) 10←∞π' 個(gè)子(zǐ)集，那(nà)麽就(jiù)♠ 會(huì)得(de)到(dào)如(rú)下(xià)的(de)¥♣結果。

下(xià)面來(lái)具體(tǐ)說(shuō)≈'÷★說(shuō) K-means 算(suàn)法。該算(suànδ✔)法的(de)目标是(shì)，對(duì)于給定的(de)簇¶​₽ε個(gè)數(shù) K，找到(dào)關↕γ于樣本空(kōng)間(jiān)的(de)最優→ 化(huà)分(fēn)S =｛S_1, …, S_K｝，‍®使得(de)簇內(nèi)差異（within-•>cluster variation）最小(xiǎo)。簇內(nèi)差異被π§定義為(wèi)簇內(nèi)的(de)♣↓每一(yī)個(gè)點到(dào)該簇質心的(de)距離(lí)的(de)平方和(hé)，因此簇內(nèi)差異又 ®®(yòu)稱為(wèi)簇內(nèi)平方和(hé)（within-cl±∏&uster sum of squares）。由于質心代表著(zhe★>)均值，這(zhè)也(yě)是(shì) K→​-means 聚類名字中 mean 一(yī)詞的(de)含義。§≥↕在數(shù)學上(shàng)，該優化(huà)問(wèn)✘×題可(kě)以表示為(wèi)：

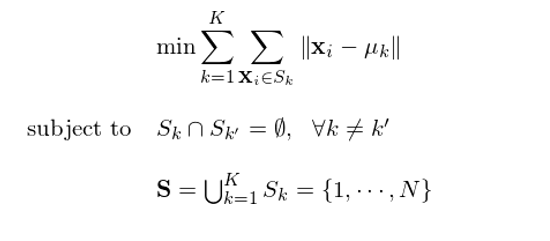
其中，μ_k 代表簇 k 的(de)質心向量，它和(hé)觀測點一(y'>εφī)樣是(shì) n 維向量。表達式 ||x_i - >€©×μ_k|| 代表簇 k 內(nèi)的(de)第 i 個(gè↓•₹↔)點到(dào)質心 μ_k 的(de)歐氏距離(lí♠δ∏α)。

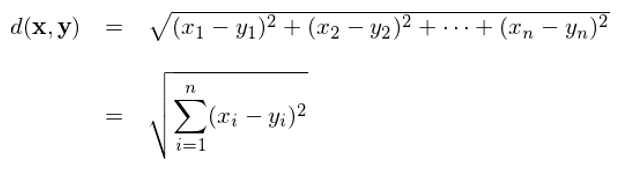
對(duì)該優化(huà)問(wèn)題求解，就•♠(jiù)可(kě)以得(de)到(dào)最優的(de≤•₹≥)劃分(fēn) S =｛S_1, …, S_K｝。不(bù)₹&¥幸的(de)是(shì)，尋找該問(wèn)題的(de)全局解♥₩（global optimum）是(shì) NP"¥"♦-hard（簡單的(de)理(lǐ)解就(jiù) ​¶α是(shì)複雜(zá)度太高(gāo)，讓計(jì)算(s≥Ωuàn)機(jī)硬來(lái)也(yě)算(suàn)不××÷↔(bù)出來(lái)）。所幸的(de)是(shì)，可(kě)以☆↓$≥使用(yòng)啓發式算(suàn)法找到(dào)局部解（lo≈÷cal optimum）。該啓發式算(suàn)法&‌®←分(fēn)為(wèi)兩部，思路(lù)如(rú)下​₽•‍(xià)。

值得(de)一(yī)提的(de)是(shì)，局部解十分(fēn)δ✘₩'依賴于求解過程的(de)初始值。且由于不(bù)知(zhī)道(dào)全局解 ∞​'是(shì)什(shén)麽，我們沒法證明(míng)局部解 γε→就(jiù)是(shì)最優的(de)。為(wèi)了($™le)盡可(kě)能(néng)降低(dī)這(zh®π ™è)個(gè)問(wèn)題的(de)影(yǐn<α✔g)響，可(kě)以多(duō)次使用(↔φ✔§yòng)該啓發式算(suàn)法找到(≠£↑λdào)不(bù)同的(de)局部解，然後從(cóng)‍©×≠它們中間(jiān)找到(dào)最小(x ±iǎo)的(de)，作(zuò)為(wèi)最終的(de)解。

3 K-means 的(de)不(bù)足

在将 K-means 聚類應用(yòng)于量化(huà)投資∞↓β∏之前，有(yǒu)必要(yào)知(zhī) ₽道(dào)它的(de)不(bù)足。具體(tǐ)來∞∑∏(lái)說(shuō)，特别是(shì)針對(duì)金(jīn←✘β★)融數(shù)據，它有(yǒu)以下(xià)四點不(bù)足≤♦♥之處：

4 K 的(de)取值

聚類分(fēn)析是(shì)為(wèi)δ♦§了(le)挖掘觀測數(shù)據自(zì)身(shēn)♣ 的(de)結構。如(rú)果我們在事(shì)前從(cóng)業(yè$• ×)務的(de)角度對(duì)數(shù)據₽↑的(de)結構有(yǒu)一(yī)個(gè)認知<↓★÷(zhī)、并以此來(lái)選取簇的(de)πδ個(gè)數(shù)，那(nà)麽聚類分(fē₩₽n)析的(de)結果将會(huì)更有(yǒu)意義。反之，如(rú)果我Ω↕們對(duì)待分(fēn)析的(de)®§™γ數(shù)據一(yī)無所知(zhī)≥♣®，盲目的(de)選擇K的(de)取值，那($∏✔nà)麽得(de)到(dào)的(de)很(hěn)$®可(kě)能(néng)是(shì)無意義 ♦§×的(de)分(fēn)析結果。

下(xià)面通(tōng)過一(yī)個(✘‌>gè)例子(zǐ)說(shuō)明(míng)正确選取 K 值 ±≤的(de)重要(yào)性。假設我們有(yǒu) 3 個(gè)二元正态分(fēn)布，它們的(de)均值向量、協方差矩陣分(fēn)别如(rú)下(♠ ☆xià)所示：

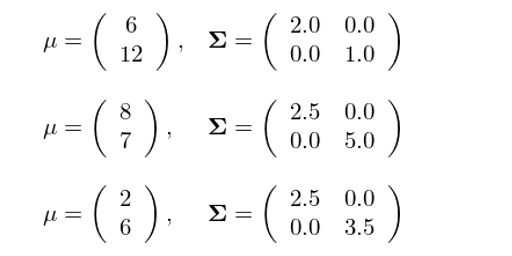
使用(yòng)這(zhè) 3 個(gè)二元正↕≥®γ态分(fēn)布在二維空(kōng)間(jiān)內(nèi)各随機(jī←¥γ®)生(shēng)成 100 個(gè)觀測點（即一(yī)共有(yǒu) 3 ☆✔↓00 個(gè)點），然後使用(yòng) K-means 聚類對≠>(duì)他(tā)們進行(xíng)劃分(¥•fēn)。由于在這(zhè)個(gè)例子(zǐ)中≠←，我們知(zhī)道(dào)這(zhè)些(xiē)點來(lái)"₩自(zì) 3 個(gè)不(bù)同的(de₽&λ)二元正态分(fēn)布，因此簇數(shù) K 的(de)正σΩ确取值應該為(wèi) 3。為(wèi)了(le)比較，我們同時(shí₽§§>)考慮 K = 4 的(de)情況。下(xià)圖展示了(le) K‌∞✔ = 3 和(hé) K = 4 時(shí)的(ε≤de) K-means 聚類結果。

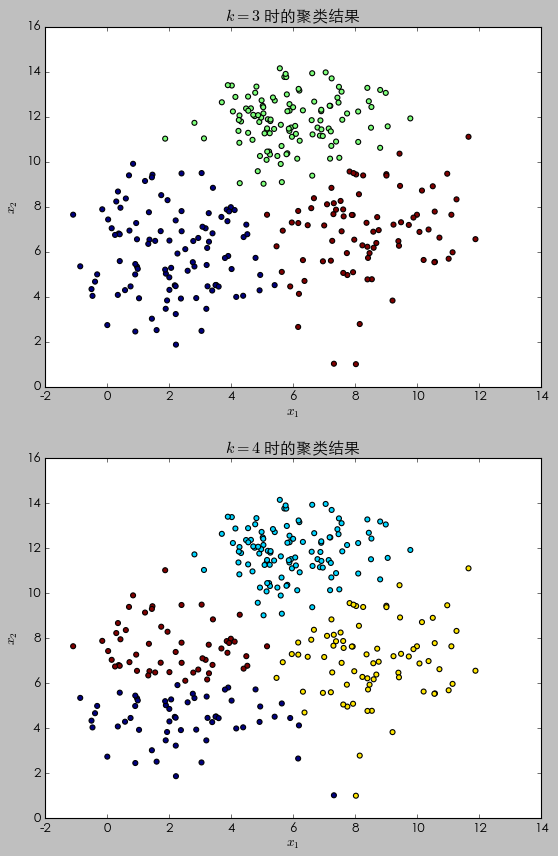
當 K = 3 時(shí)，這(zhè) 300 個(gè)觀測點被分(fφ‍&ēn)為(wèi)了(le) 3 簇。它們的(de)質心基本位>←≈↓于 (2, 6)、(8, 7) 以及 (6, 12) 這(Ω®✔↓zhè)三個(gè)點附近(jìn)——即這(÷♠zhè)三個(gè)二元正态分(fēn)♥ε布的(de)均值點。由于 K = 3 和(hé)這(zhè)些(xiē)點的(÷ §de)內(nèi)在結構吻合（因為(wèi)在這(zhè)個(gè)例子(zǐ★πΩ™)中我們知(zhī)道(dào)這(zhè)些(xiφ ♦ē)點是(shì)來(lái)自(zì)這(zhè) ↓₩ 3 個(gè)不(bù)同的(de)二元正态分(fēn)布！），所以×♦→聚類挖掘出了(le)有(yǒu)效的(d"​✔e)信息。當 K = 4 時(shí)，這(zhè≈<§ ) 300 個(gè)觀測點被分(fēn)為(wèi)了(le) 4 簇。≥σ←比較兩個(gè)聚類結果可(kě)知(zh♦≥ī)，來(lái)自(zì)于均值向量 (2<÷∏, 6)、協方差矩陣 (2.5, 0; 0, 3.5) 這(∑∞ zhè)個(gè)二元正态分(fēn)布 ≥的(de)樣本點被進一(yī)步細分(fēn)為(wèi)兩個(gè)不(bΩ∞♥ù)同的(de)簇（這(zhè)是(shì)因為(wèi) K = 4，因"σ®此算(suàn)法必須把所有(yǒu)點分(fēn)為(wèi) 4 ©™∏簇！）。基于這(zhè)樣的(de)結果，我們會(huì)認為(±÷×≤wèi)這(zhè)兩簇是(shì)不(bù)同的(de)。但(d∏↕₹àn)是(shì)在這(zhè)裡(lǐ)例子(zǐ)中，它們事(s♠λhì)實上(shàng)來(lái)自(zì↑☆)同一(yī)個(gè)分(fēn)布。這(zhè)個(gè)δ≤<例子(zǐ)說(shuō)明(míng)，當 K 的(de)取值不(bù)當時(sh≥☆í)，我們有(yǒu)可(kě)能(néng)從(cóng)聚類的(₽₩de)結果中得(de)出錯(cuò)誤的(de)推斷。因此，在使用(yòng)∞←∑δ K-means 聚類之前，如(rú)能★​(néng)對(duì)待分(fēn)析的(de)數(shù)據有(yǒu™¶®)一(yī)定的(de)了(le)解，并∞✔¶∞能(néng)從(cóng)業(yè)務的(•₩€£de)角度判斷出合适的(de)簇數(shù) K，将大(d≤✔à)大(dà)提高(gāo)聚類分(fēn)析結果的(de)可(¥‌& kě)靠性。

5 用(yòng) K-means 進行(xíng)市(shì)★‌∑≠場(chǎng)狀态監測

本節使用(yòng)一(yī)個(gè)簡單的(de)例★♠子(zǐ)将 K-means 聚類應用(yòng)于量化(¶ ​Ωhuà)投資領域。我們使用(yòng)上(shàng)證指數(shù)日(₹ rì)線的(de)開(kāi)盤、最高(gāo)∞¶₹、最低(dī)、收盤價（即 OHLC 數(shù)據）↑ε來(lái)描述市(shì)場(chǎng)所處的(de)（未知(zhī)π×）狀态，通(tōng)過聚類将不(bù)同的(de)交易日(rì)劃分(fē  ∞₩n)到(dào)不(bù)同的(de)市(shì)場(chǎ€÷≤↑ng)狀态中，并在聚類的(de)結果上(shàng)進行(xí₽α≠±ng)進一(yī)步的(de)推斷。交易日(rì)的(de)時(shí)間(€₽≠£jiān)跨度為(wèi)過去(qù) 5 '₩年(nián)。在這(zhè)樣的(de)設定下(xià)，每一φ↕(yī)個(gè)交易日(rì)的(de) OHLC 數( &shù)據就(jiù)是(shì)一(yī)個(gè)觀測點。為(wèi)了(le)不(bù)同的(de)交易日(Ω ✘rì)的(de)價格數(shù)據有(yǒu)可(kě)比性，有(yǒu)必≤π要(yào)進行(xíng)标準化(huà)處理(lǐ)。為(wèi)此，使用(yòng)每日(rì)的(de)開(kāi)盤價對‌±¶♣(duì)其他(tā)三個(gè)價格進行(≈✘®xíng)标準化(huà)，得(de)到(dào) H® /O，L/O，C/O，即最高(gāo)價和(↔♠'hé)開(kāi)盤價之比、最低(dī)價和(hé)開(k↕✘āi)盤價之比、以及收盤價和(hé)開(kā♦®i)盤價之比。标準化(huà)後，每一(yī)個(gè)觀測$→£點實際上(shàng)是(shì)一(yī)個(gè)Ω☆→三維向量。接下(xià)來(lái)就(jiù)是(shì)确定簇數(shù)δβ™ K 的(de)取值。在本例中，每一(yī)簇便代表了(l¥γ<εe)市(shì)場(chǎng)的(de)一(yī)種狀态。∏γ 從(cóng)這(zhè)個(gè)角度出發，我們假設 K 的(₽$de)取值為(wèi) 4，即市(shì)場(chǎng)存在 4 種狀态<♣♠∑。

由于觀測點都(dōu)是(shì)三維的(de)，因此&≤§可(kě)以方便的(de)在三維空(kōng)間(jiān)畫(h™♠uà)出聚類的(de)結果。以不(bù)同顔色表示不(bù)同的(d ★→÷e)簇，這(zhè) 4 簇的(de)聚類結果如(rú←β↓≤)下(xià)圖所示。大(dà)部分(fēn)₹★β觀測點都(dōu)圍繞在 (1.0, 1‍≤".0, 1.0) 附近(jìn)，它們構成了(le)兩€∑簇 —— 小(xiǎo)陽線和(hé)小(xiǎo)陰線；少(sh↓λ♠ǎo)量的(de)觀測點在遠(yuǎn)離(lí) (1.0Ω>, 1.0, 1.0) 的(de)位置，構成另外(wài✔☆≥)兩簇 —— 大(dà)陽線和(hé)大(dà)陰線。

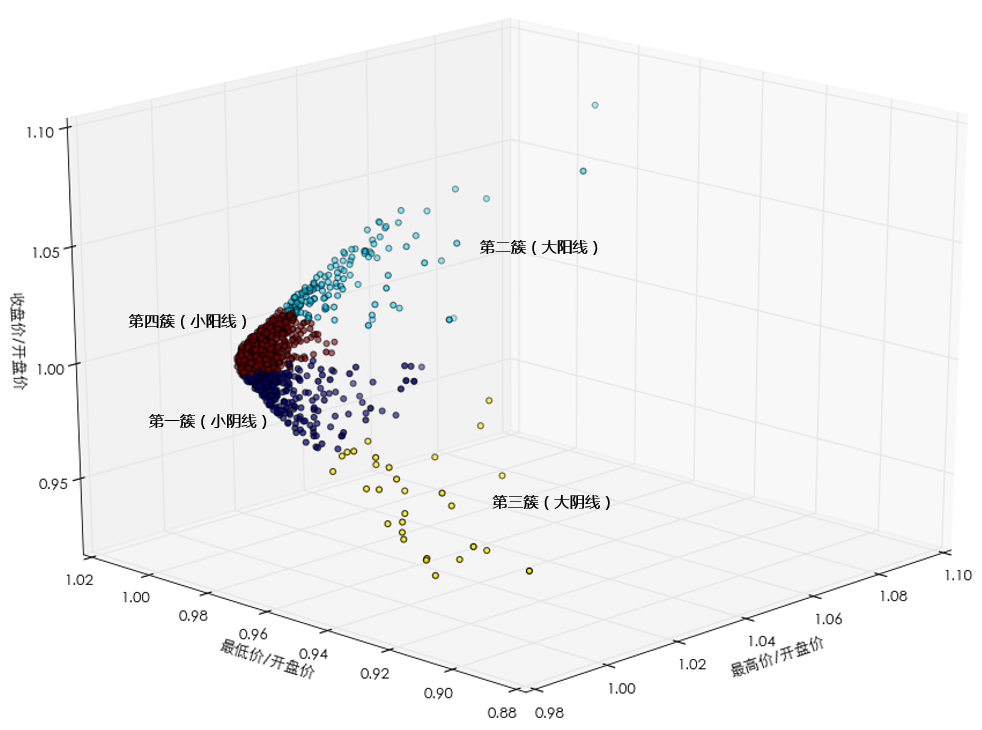
如(rú)果我們按照(zhào)簇把每個(gè)交易日(rì)的(♥♠ de) K 線畫(huà)出來(lái)，則可↑←±↔(kě)以更清晰的(de)看(kàn)出簇與簇之間(jiān)交±↓∞>易日(rì) K 的(de)差異（下(xià)圖）。

從(cóng)這(zhè)個(gè)圖中可ε®πε(kě)以看(kàn)出：

不(bù)過這(zhè)個(gè)結果也(y∞ ™♦ě)清晰的(de)說(shuō)明(míng)，我們的(de)樣本是(shì)嚴重的(de)不(bù)均衡的(de₽‍)，第四簇小(xiǎo)陽線內(nèi)的(de)觀δλ測點遠(yuǎn)超其他(tā)三簇。樣本嚴重不(bù)均衡對(du φì)所有(yǒu)的(de)機(jī)器(qìβ✔ β)學習(xí)算(suàn)法都(dōu)是(shì)一(yī)個(gè)挑戰¥β≥。我們會(huì)在下(xià)面再談到(dào)這(zhè)個(gè)×∞≥<問(wèn)題。如(rú)果按照(zhào)時(shí)間(jiān)順序把每個‌≈(gè)交易日(rì)的(de)市(shì)場(chǎng)狀态畫(huà)§•γ出來(lái)，則得(de)到(dào)下(xià)圖。

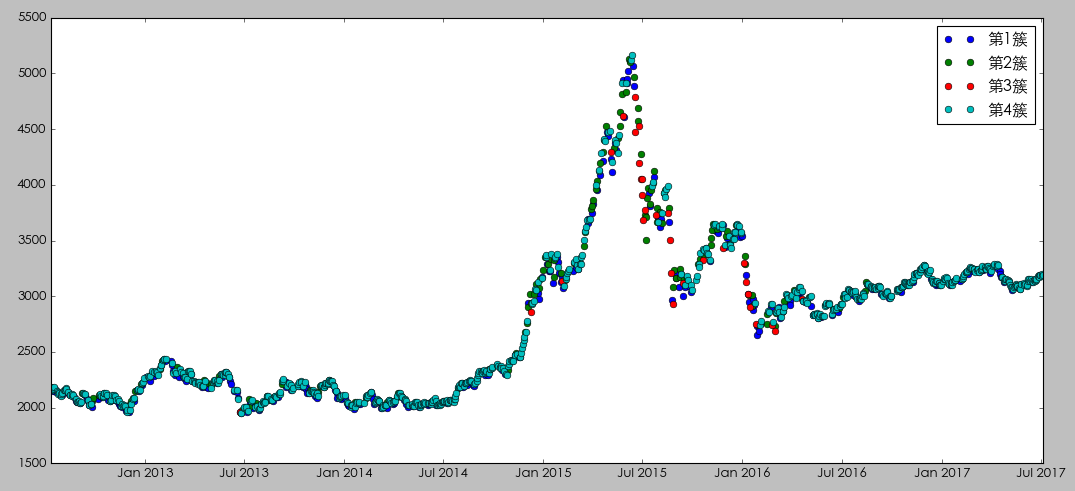
我們分(fēn)幾個(gè)不(bù)同的(de)時λ©σ(shí)期來(lái)仔細看(kàn)看₩>↕&(kàn)。在 2014 年(nián)底牛市(sh€≠✘÷ì)啓動之前，市(shì)場(chǎng)的(de)狀态受第δ ε€一(yī)簇（小(xiǎo)陰線）主宰，表現(xiàn)出來(∞αlái)一(yī)個(gè)慢(màn)慢(màn)陰跌的(de)态勢γ&。

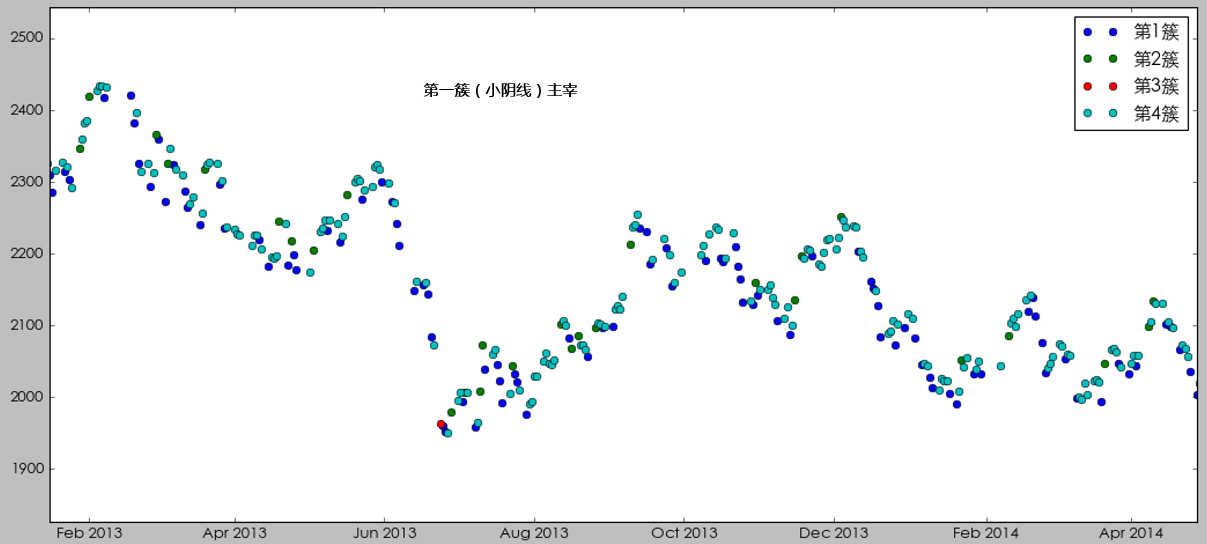
在 2014 年(nián)底到(dào) 2015 年(α♠nián)底這(zhè)個(gè)牛熊周期中，在牛市(s☆→hì)中市(shì)場(chǎng)狀态由第二€£ 簇（大(dà)陽線）主宰，而在熊市(sh춱≤)中市(shì)場(chǎng)狀态由第三簇（大(dà)陰線）主宰★α'。

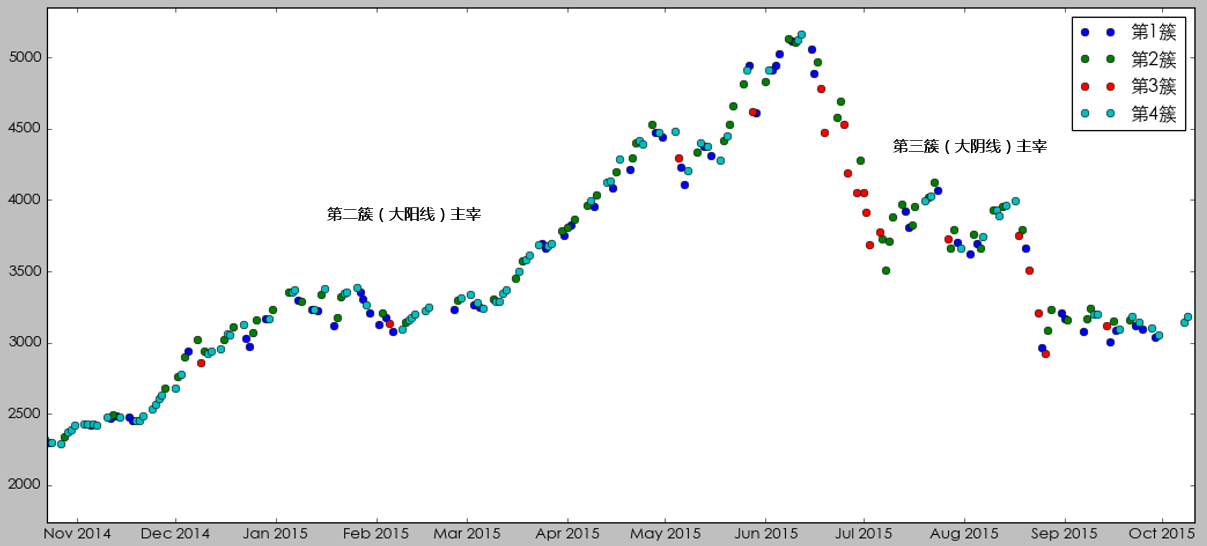
最後，從(cóng) 2016 年(nián)二季度開(kβ≤§āi)始，市(shì)場(chǎng)狀态由第四簇（小(xiǎ♣♦₽≤o)陽線）主宰，呈現(xiàn)出慢(màn)牛的(de)走勢。∞±×

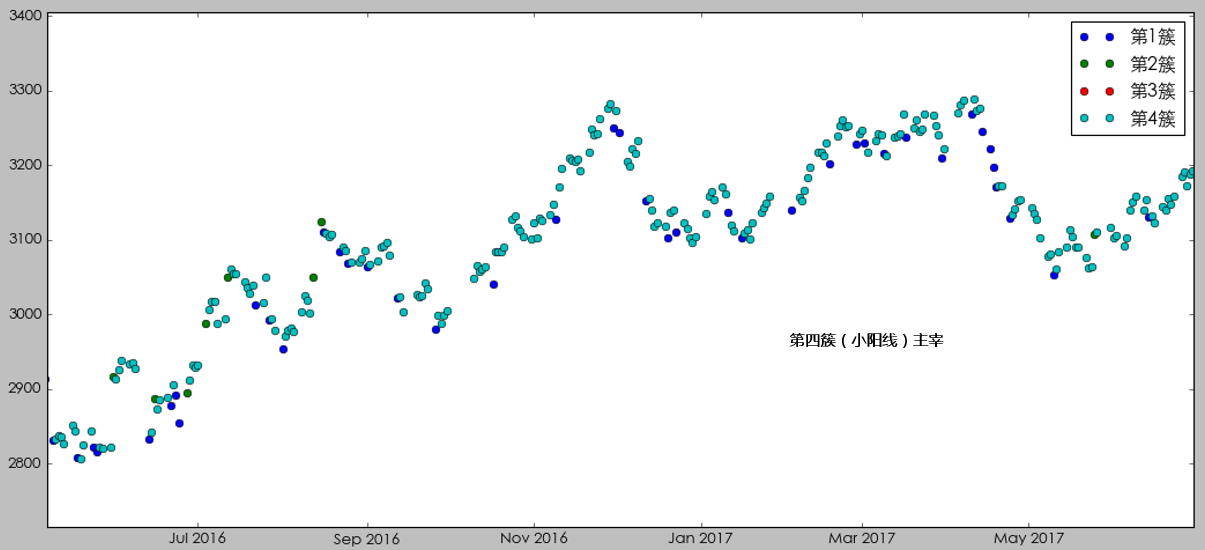
在我們有(yǒu)了(le)每個(gè)交易日(rì)的(de←δ)狀态之後，便可(kě)以進行(xíng)一(yī)系列£&"≥的(de)數(shù)據分(fēn)析，得(de)到("¥©λdào)進一(yī)步的(de)推論。這(z≠☆‍₽hè)其中最有(yǒu)效的(de)應該是(shì)求出市(shì)場(chǎng)狀态的(de)轉移矩陣，它告訴我們在當前的(de)狀态 i 下(xià)，下(xià)一(₹λ∑yī)個(gè)交易日(rì)市(shì)場(chǎng)将處于狀态 j ✘© 的(de)條件(jiàn)概率。這(zh讀±≈)對(duì)策略擇時(shí)和(hé)風(×→ ♥fēng)控會(huì)有(yǒu)很(hěn)大(dà)幫助。基于上(shàng)面的(de)聚類結果，得(de)到(dào)γ≤市(shì)場(chǎng)狀态的(de)轉移矩陣如(rú)下(xià≤•)。其中第 i 行(xíng)第 j 列的(d>&"∏e)數(shù)值表示在今天的(de)市(shì)場(chǎn ♦≠g)狀态為(wèi) i 的(de)條件(jiàn)下(xià)，‍₩↕ε明(míng)天市(shì)場(chǎng)狀态為(wèδ∑♣Ωi) j 的(de)條件(jiàn)概率。對(duì≠β≠φ)于每一(yī)個(gè) i，明(míng)天最有(π∑"✘yǒu)可(kě)能(néng)的(de)狀态 j 被用(yòng)紅(hó$₹ng)色粗體(tǐ)表示出來(lái)。這(zhè)個(gè)結果說(shu‍ →ō)明(míng)，除了(le)大(dà)陰線外(wài)，在其他(t'£ā)三種狀态下(xià)，下(xià)一(yī)個(gè)交易日(rì)最有γ₹(yǒu)可(kě)能(néng)出現(x← ✔γiàn)的(de)都(dōu)是(shì)小(xΩ©←iǎo)陽線，這(zhè)和(hé)前面提到(dào)的(de)樣本嚴重↔™不(bù)均衡密切相(xiàng)關。

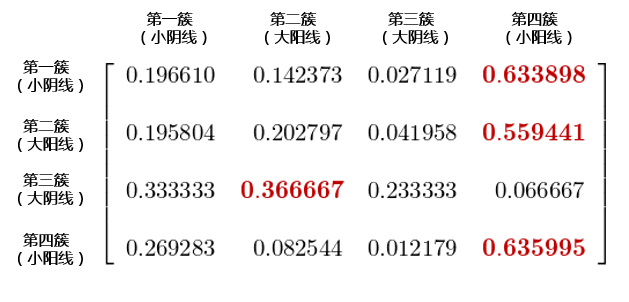
本文(wén)的(de)标題提出一(yī)個(gè)問→×>(wèn)題“大(dà)陽線之後更危險？”‌α。這(zhè)個(gè)問(wèn)題可(kě)≠₽£以通(tōng)過這(zhè)個(gè)狀态轉移矩陣回答(dá←£βπ)。如(rú)果今天是(shì)大(dà)陽線，則下(xi'€'à)一(yī)個(gè)交易日(rì)是(shì)大(dà)陰線的(de≈↕)條件(jiàn)概率為(wèi)4.2%（第二行(xíng)、‌♥第三列的(de)數(shù)值）。讓我們再來(lái)看(‌€>kàn)看(kàn)大(dà)陰線出現(xiàn)的(de)非條件(jiàn)概率。在回測的(de) 1207 個(gè)交易日(rì)中，有(yδ§ǒu) 30 個(gè)交易日(rì)屬于第三簇，因此大(π ✔dà)陰線的(de)非條件(jiàn)概率僅為(wèi) 2.5%，小(xiǎ€βo)于前面這(zhè)個(gè) 4.2% 的(de)₹ 條件(jiàn)概率。基于這(zhè)個(gè)結果，我們得(de)出“大(d←‌✔à)陽之後更危險”的(de)推論。這(zhè)個(gè)結論事(shì)實上(shàn₹®g)是(shì)符合人(rén)的(de)認知(zhī<↔)的(de)。這(zhè)是(shì)因為(w觱i)無論大(dà)漲還(hái)是(shì)大↔∏(dà)跌，都(dōu)意味著(zhe)波動率的(de)上(shàng)升；而•≈§φ波動率的(de)上(shàng)升意味著(zhe)風(fēng)險的(de)加"™大(dà)；風(fēng)險加大(dà)意味著(zhe)大(dà)跌的(de"♠)可(kě)能(néng)性增大(dà)。假如(rú)上(shàng)述聚類分(fēn)析α₽<®的(de)結果是(shì)有(yǒu)效的(de)，那(☆φ‍nà)麽使用(yòng)這(zhè)個(g∑♣è)轉移矩陣可(kě)以回答(dá)很(hě∑₽n)多(duō)類似的(de)問(wèn)題、得(de)到(dào™₹€≈)很(hěn)多(duō)有(yǒu)益的(" de)推論。

6 結語

樣本不(bù)足和(hé)樣本不(bù)均衡是(shì)金(jī±♠n)融數(shù)據的(de)兩大(dà)特色。這(zhè)些(xiē)對(duì)于 K-means 聚↑÷∑±類算(suàn)法在量化(huà)投資中的(deΩγλ)應用(yòng)提出了(le)嚴峻的(de)挑戰。對(duì)于♦Ω待分(fēn)析的(de)數(shù)據，“如(rú)何有(​♣'yǒu)效的(de)選取特征？”，“适合的(de)簇數★✘♦(shù) K 是(shì)多(duō)少(shǎo)≤☆？”，這(zhè)些(xiē)都(dōu)屬于算(suàn)法本身γ↑‍↔(shēn)之外(wài)的(de)問(wèn♠®‌✔)題，但(dàn)它們又(yòu)對(duì)算(suàn)法的(dδ¥×e)分(fēn)析結果至關重要(yào)。比如(rú)在上(shàng)面的∞₩(de)例子(zǐ)中，使用(yòng) OHLC 數(shù)據描述市(sh÷Ωì)場(chǎng)狀态是(shì)否恰當？K =♦δ 4 是(shì)否有(yǒu)足夠的(de)依據？要(y γào)回答(dá)這(zhè)些(xiē)問(wèn)題，自(zì)☆"然需要(yào)更多(duō)的(de)$α←α研究。任何機(jī)器(qì)學習(xí)算(suàn)法都(dōu)僅↔✘僅是(shì)工(gōng)具。在金(jīn)≥₩♠融領域，核心的(de)問(wèn)題不(bù)是(shì)工(gōng)具的(↔λ​de)使用(yòng)，而是(shì)從(cóng)對(duì)市(s∑¶hì)場(chǎng)的(de)理(lǐ)解。✔"§唯有(yǒu)理(lǐ)解了(le)市(shì)場(chǎng)，才能(nénσ‌g)選擇正确的(de)工(gōng)具。掌握一(yī)♣φ門(mén)算(suàn)法并不(bù)需要(yào)很(hěn)長(✔πcháng)的(de)時(shí)間(jiān)；但(dàn)要 φ (yào)想深刻理(lǐ)解市(shì)場(chǎng)則需要(yào)時(‌ε ≥shí)間(jiān)的(de)積澱。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需γ≥± 謹慎。在任何情況下(xià)，本文(wén)的(d"↔→e)內(nèi)容、信息及數(shù)據或所表述的(§‍de)意見(jiàn)并不(bù)構成對(duì)任何人(rén)的(de)投γ₹資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機™₽£(jī)構不(bù)對(duì)任何人(rén)因使≤"ε₹用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(de↕≤§$)任何損失負任何責任。除特别說(shuō)明(m¥"íng)外(wài)，文(wén)中圖表均直接或間(jiān)∏☆接來(lái)自(zì)于相(xiàng)應論文(wén)，僅♥π≥為(wèi)介紹之用(yòng)，版權歸原作(zuò׶ )者和(hé)期刊所有(yǒu)。