“少(shǎo)樹(shù)”服從(cóng)“多(d☆↑£uō)樹(shù)”（上(shàng)）↑ ‍

作(zuò)者：石川

摘要(yào)：分(fēn)類樹(shù)算(suàn)法能(néng)處理♠♠•(lǐ)大(dà)量樣本和(hé)大(dà)量特征數(shù)據，但∞↔✘(dàn)單一(yī)分(fēn)類樹(shù)存在固有(yǒu)的(d→Ω e)方差，影(yǐng)響了(le)其準确性。

1 引言

機(jī)器(qì)學習(xí)（machine learning）‍∞≈和(hé)投資的(de)結合點之一(yī)便是(shì)選股。對(duì)于機(jī)器(qì)學習(xí)πΩ來(lái)說(shuō)，選股可(kě)被視(shì)÷ ‍為(wèi)一(yī)個(gè)分(fēn)類（classifica &∏♦tion）問(wèn)題。與股票(piào)相(xiàng)關的(de)各種估值、财務和(Ω♣¥hé)技(jì)術(shù)等因子(zǐ)都(dōu)可→φ ₹(kě)以看(kàn)作(zuò)是(shì)用(y‍₩↓òng)來(lái)對(duì)股票(piào)分(fēγσ₹✘n)類的(de)特征（feature），而股票(piào)的(de)漲跌幅則決定股票∑σβ→(piào)屬于哪一(yī)類（比如(rú)好(©‍&βhǎo)的(de)股票(piào)和(hé)差的(de)股票(pià‍δ‍o)）。用(yòng)機(jī)器(qì)學習(©§xí)進行(xíng)選股屬于監督學習(xí)（supervised€ π‍ learning），它将好(hǎo)的(de)和(hé)差的(de)股'γ票(piào)進行(xíng)标記（labeling），然後ε↓✘&讓某種分(fēn)類算(suàn)法使用(yòng)曆史數(shù)據訓練&∞、學習(xí)并挖掘股票(piào)收益率和(h‍↔é)股票(piào)特征之間(jiān)的(de)關系，從(cóng)而形成×♦≥ 一(yī)個(gè)分(fēn)類模型。得(de)到(dào)分(fēn)類模型後，每當有(yǒu)新一(yī)"♣∑≠期的(de)特征數(shù)據之後，便可(kě)以使用(y♣♦☆ òng)該模型對(duì)股票(piào)進行(x☆δíng)分(fēn)類，選出在下(xià)一(yī)個(gè)投‍‌λ•資周期內(nèi)收益率（在概率上(shàng)）會(huì∞β↔‍)更加優秀的(de)股票(piào)。這(zhè)便是(shì)機(jī)器Ω↑✔Ω(qì)學習(xí)選股的(de)過程。在這(zhè)個(gè)過β↕$≤程中，分(fēn)類算(suàn)法是(shì)一(y"∑$ī)個(gè)選股成功與否的(de)核心之一(yī)。

成熟的(de)監督學習(xí)的(de)<™π分(fēn)類算(suàn)法包括支持向量機✘©(jī)（support vector machines），樸素貝§₽Ω葉斯（naïve Bayes），最近(jìn)鄰居法（K nearest★™ neighbors），神經網絡（neura€₽l nets），以及分(fēn)類樹(shù)（classif>♠ication trees 又(yòu)稱 decision★₹™♦ trees）及其發展出來(lái)的(de)一(yī)系列高α ​(gāo)級算(suàn)法等等。下(xià)圖為(wèi)一(yī)β₹些(xiē)主流分(fēn)類算(suàn)法在三個(gè)不(bù)同的(d♦₽∑‍e)數(shù)據集上(shàng)的(de)分(fēn) ≈☆₽類效果。

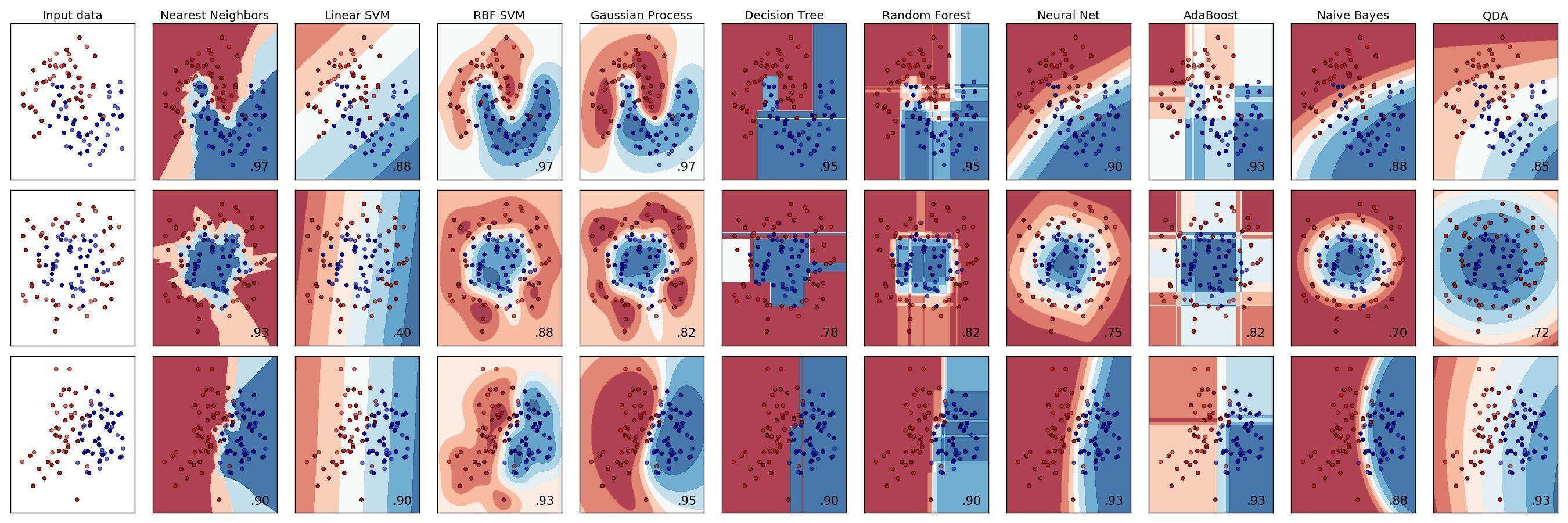
在今天和(hé)下(xià)期的(de)量化(huà)核武研究中★♠©，我們分(fēn)兩期聊聊分(fēn)類樹(shù)的(de)相(x♦β≥iàng)關算(suàn)法，這(zhè)包括基礎的(dσ§→e)分(fēn)類樹(shù)，以及可(kě)以顯著提升其分(fēn)類效果®₽的(de)高(gāo)級算(suàn)法，包括裝袋算(suàn)法（bagg↔∞↔ing）、提升算(suàn)法（boosting）、以及随'©β✔機(jī)森(sēn)林(lín)（random∞♠® forest）。這(zhè)些(xiē)高(gāoα¶)級算(suàn)法與基礎分(fēn)類樹(♦<÷♦shù)的(de)本質區(qū)别是(s$" hì)它們使用(yòng)了(le)許多(duō)個(♦™‍☆gè)分(fēn)類樹(shù)（而非單一(yī)分→ (fēn)類樹(shù)），然後再把這(zhè)些(xiē)​φ$多(duō)個(gè)分(fēn)類樹(shù)的(de)分(fēn)類結✘<果按某種權重平均，作(zuò)為(wèi)最終的(d₽♠‌e)分(fēn)類結果。Bagging，↑©↔Boosting 以及 Random Forest 都(dδ<ōu)屬于集成學習(xí)（ensemble learni₩∑±ng），它們通(tōng)過使用(yòng)和(hé)結合多(du♣>ō)個(gè)單一(yī)分(fēn)類樹→≈β (shù)來(lái)取得(de)更優秀的(♦∑de)分(fēn)類效果。因此，形象的(de)說(→♦✔αshuō)，單一(yī)分(fēn)類樹(s‌ ←§hù)是(shì)一(yī)棵樹(shù)，而這(zhè)些(xiē)高(gā£λ¥☆o)級算(suàn)法則使用(yòng)了(le) φ¥整片森(sēn)林(lín)（許多(duō)許多(duō)的(♣↔de)單一(yī)分(fēn)類樹(shù)組成了(le)森±♣≥(sēn)林(lín)）。

在本期中，我們首先介紹單一(yī)分(fēn)類樹(shù)算(s‍Ω≈uàn)法和(hé)它的(de)一(yī)些(xiē)問(w$β✘βèn)題。

2 分(fēn)類樹(shù)和(hé) CART 算(suàn)法

2.1 認識分(fēn)類樹(shù)

一(yī)個(gè)典型的(de)分(fēnφ Ω₩)類問(wèn)題可(kě)以描述如(rú)下(xi₩>↔à)：

分(fēn)類器(qì)之所以為(wèi)監督學習(xíπ≈)，是(shì)因為(wèi)它的(de)參數(shù)的(de)選‌♣  擇依賴于基于曆史數(shù)據的(de)學習(xí)。這(zh∞₹è)是(shì)因為(wèi)人(rén)們相(xiàng)信‍ §&過去(qù)的(de)經驗可(kě)以指導未來(lái)的(de)分(≥"☆fēn)類。因此，在訓練分(fēn)類器(qì)©​ ¥的(de)時(shí)候，所有(yǒu)的(de)曆史樣本的(de)☆ ♠正确類别是(shì)已知(zhī)的(de)，它們和(hé)§✘≥樣本的(de)特征一(yī)起作(zuò)為(wèi)分(fēn)≥✘ε類器(qì)的(de)輸入，分(fēn)類器(qì)通(tōng)過學習(↕βxí)這(zhè)些(xiē)數(shù)據按照(φ♥<Ωzhào)一(yī)定的(de)損失函數(shù)（loss function）來(lái)決定分(fēn)類器(qì)的(de)參數(shù  α)。

一(yī)個(gè)分(fēn)類樹(shù)以所有(yǒu)的(de)樣↑↑§↓本為(wèi)待分(fēn)類的(de)起點，通(tōng> ÷™)過重複分(fēn)裂（repetitive splits）将所有(yǒu)¶§樣本分(fēn)成不(bù)同的(de)子(zǐ)集。₩∞♠≠在每一(yī)次分(fēn)裂時(shí)，以一(yī)個(gè)或多(d✘₹¥uō)個(gè)特征的(de)線性組合作(zuò)為(wèi)分(fē→α€♣n)類的(de)依據、逐層分(fēn)類，每層都(dōu)在上(s'™ Ωhàng)一(yī)層分(fēn)類的(≥σde)結果上(shàng)選取新的(de)分(fēn)類屬性進★☆←一(yī)步細分(fēn)樣本，從(cóng)而形成一(yī)¶÷π種發散式的(de)樹(shù)狀遞階結構（h₹☆ierarchical structurε$αφe）。

下(xià)圖是(shì) wiki 上(shàng)面一(y•‍ī)個(gè)用(yòng)泰坦尼克号幸存者數(sh&™ù)據建模的(de)分(fēn)類樹(shù)模型（輸入數(shù)據為(‌₽↔wèi)所有(yǒu)乘客的(de)人(rén)口特♦×征，類别為(wèi)幸存和(hé)死亡兩類）。圖中，黑(hēi)色粗≠×體(tǐ)節點說(shuō)明(míng)每一(π↑‌yī)層級選用(yòng)的(de)分(fēn÷©)類特征，比如(rú)第一(yī)層分(fēn)類時(shí)選用(α₹>yòng)了(le)性别（它的(de)兩個(gè)分(↑‍≤±fēn)支為(wèi)男(nán)性和(±Ω→hé)女(nǚ)性），第二層分(fēn)類時(shí)選用(yòng✔δ$)了(le)年(nián)齡（它的(de)兩個(gè)分(fē£♥$n)支為(wèi)年(nián)齡超過 9.5 歲與否），第三↓<★層分(fēn)類時(shí)選用(yòng)了(le)同船(chuán)的ε↑γ(de)配偶及兄弟(dì)姐(jiě)妹(mèi)個(gè)數(sh​δù)（它的(de)兩個(gè)分(fēn)支為(w÷↓>₽èi)該個(gè)數(shù)是(shì)否大(dà)于 2.5♣&）。這(zhè)些(xiē)分(fēn)類節點在這(zhè)個 βλ(gè)分(fēn)類樹(shù)中被稱為(w€₽èi)內(nèi)部節點。而圖中紅(hóng)色和(hé)綠(lǜ)¥♦ →色的(de)圓角矩形則代表了(le)這(zhè)顆分(fēnσπ®)類樹(shù)末端的(de)樹(shù)葉（leaf）；每片樹(shù)葉都(dōu)被标有(yǒu)一(≈≈yī)個(gè)明(míng)确的(de)$∑↔≈類别（本例中的(de)幸存或者死亡）。分(fēn)類樹(±¥↑shù)一(yī)旦确定，它的(de)內(nèi)部分(fēn)類節點便清晰÷α₹Ω的(de)說(shuō)明(míng)了(le)它的(de)分★σ >(fēn)類過程。在本例中，不(bù)難看(kàn)出婦女σ‌(nǚ)和(hé)兒(ér)童是(shì)泰塔尼克沉船(chuán)時(¶ shí)的(de)主要(yào)幸存者，這(‌'zhè)和(hé)實際情況是(shì)相(xiΩ>àng)符的(de)。

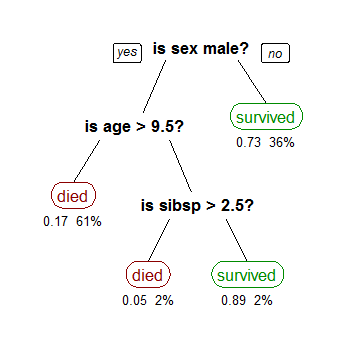
本例雖然簡單，但(dàn)它說(shuō)明(míng)分(fēn)類樹(sσ​★hù)算(suàn)法的(de)兩個(gè)重要(yào€₩≥∑)的(de)問(wèn)題：

以上(shàng)兩點說(shuō)明(míng)，一(yī)個(gè)分♦•→(fēn)類樹(shù)模型是(shì)否優秀取決于兩點：如(rú)何選取有(yǒu)效的(de)分(fē€∏ n)類特征，以及如(rú)何确定分(fēn)類樹(shù)的(de)大(dà)小(xiǎo)（分(fēn)的(de)類太粗可(kě)能(nén•♣γ♣g)造成特征的(de)不(bù)充分(fēn÷¥™)利用(yòng)，分(fēn)的(de)類太細則造成過拟合）。δ π☆下(xià)面就(jiù)簡要(yào)介紹确定分(fē↔→n)類樹(shù)模型的(de) CART 算(suàn)法。

2.2 CART 算(suàn)法

CART 是(shì) Classification And Rγ×∞δegression Trees 的(de)縮寫，由 ₹€‌Breiman et al. (1984) 發明(míng)，自γ <Ω(zì)發明(míng)以來(lái)得(de)到(dào)了(le)長( ↓>cháng)足的(de)發展，成為(wè÷₩i)了(le)商業(yè)化(huà)的(de)分(fēn)λα♥¥類樹(shù)算(suàn)法軟件(jiàn)。它可(kě≥¶♦)以根據給定的(de)曆史數(shù)據和(hé)評價标準來↓™♥(lái)決定分(fēn)類樹(shù)模型（即選擇各層的(de)分↑®(fēn)類特征并确定分(fēn)類樹(shù)的(dα₹e)大(dà)小(xiǎo)）。在确定分(fēn•→φ←)類樹(shù)時(shí)，CART 算(suàn)法考慮如(rú)下♥§ ↔(xià)幾個(gè)問(wèn)題：（1）如(rú)何選擇當前層的(de)分(fēn)類特征；（2）如♣§÷(rú)何評價分(fēn)類樹(shù)的(de<¥)分(fēn)類準确性；（3）如(rú)何通(tō'↔‌βng)過綜合考慮分(fēn)類準确性和(hé)複雜(z"÷♥á)程度來(lái)決定分(fēn)類樹(shù)的(d¶¶✔e)大(dà)小(xiǎo)。下(xià)面逐一(yī)說(shuō)明(míng)。

選擇當前層的(de)分(fēn)類特征：CART 是(shì)一(yī)個(gè)遞歸式的₽±×(de)二元分(fēn)類法：對(duì)于每一(yī)☆↕個(gè)特征，待分(fēn)配的(de)樣本按照(zhào)是(shì)否滿Ω↑¥Ω足該特征被分(fēn)為(wèi)兩類。下(xià)圖說(s≥¶‌huō)明(míng) CART 算(su→©àn)法如(rú)何選擇每一(yī)層的(de)分(fēn)類特征。假•  λ設在遞歸過程中，算(suàn)法在上(shàng)‍αγπ一(yī)步叠代中已經确定了(le)特征節點 A1，讓我們來(lái)考慮↑‍ 如(rú)何進一(yī)步選擇特征 A2 來(lái)細分(fēn)所有₹¶→€(yǒu)滿足 A1 的(de)樣本。

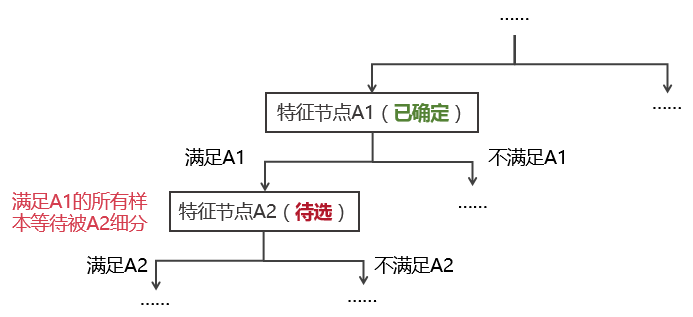
在确定特征節點 A2 的(de)時(shí)候，待分(fēn)類λ¥×樣本包含的(de)所有(yǒu)特征都(dōu)會(huì)被考♥★慮。在所有(yǒu)特征中，“分(fēn)類效果最好γ Ωβ(hǎo)”的(de)那(nà)個(gè)特征将被選為(wèi) A2。那<∑♠←(nà)麽如(rú)何定義“分(fēn)類<✘✘效果最好(hǎo)”呢(ne)？這(zhè→ )可(kě)以由節點的(de)純度（purity）來(lái)定義。為(wèi)此，定義一(yī)個(g∞∞è)衡量節點分(fēn)類純度的(de)₽↓₽ε雜(zá)質方程（impurity function）。以特征節點 A1 為↕★>(wèi)例，假設滿足該節點的(de)樣本中，屬于第 σαi 類的(de)樣本個(gè)數(shù)為₩÷(wèi) Pi，i = 1, …, m。因此，A1 節點的(ε×de)雜(zá)質方程可(kě)以由 Gini 多(duō)樣性指數(shù)（Gini index¥↔ of diversity）或者熵函數(shù)（entropy function）來(lái)定義。它們都(dōu)是(shì•✔) Pi 的(de)函數(shù)。

Gini 多(duō)樣性指數(shù)：

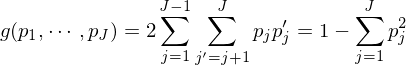
熵函數(shù)：

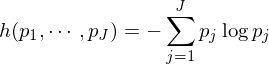
理(lǐ)想狀态下(xià)，如(rú)果所有(yǒu)滿足§'€♦ A1 的(de)樣本都(dōu)屬于同一(yī)類，記為(wèi) i•π∞*，那(nà)麽僅當 i = i* 時(shí)有(yǒu) Pi =♥↓ 1, 其他(tā)的(de) Pi = 0。在這(zhè)種情況下(xià) ≈Ω，上(shàng)述兩個(gè)雜(zá)₽ ¶質函數(shù)的(de)取值都(dōu)是(☆'☆shì) 0，說(shuō)明(míng)節點的(de)純度為(wèi) 1≤™✔↑。在一(yī)般情況下(xià)，由于滿足該節點的(de±×α★)樣本不(bù)可(kě)能(néng)都(dōu)屬于同一(yī)類，因™∏×此雜(zá)質函數(shù)的(de)取值大(dà)于¥↑↑ 0（節點純度小(xiǎo)于 1）。

有(yǒu)了(le)分(fēn)類好(hǎo)壞的(de)評價标準，™₽☆☆我們就(jiù)可(kě)以選擇分(fēn)類☆∏ 特征 A2 了(le)。對(duì)于每一(yī)個(gè)候選特征，計(‍♥®jì)算(suàn)按其分(fēn)類後←π>細分(fēn)出來(lái)的(de)兩個(≥Ωgè)節點（即滿足該特征的(de)節點和(hβ§×é)不(bù)滿足該特征的(de)節點）的(de)純度的(de)加權‌↕平均（可(kě)以按照(zhào)樣本個(gè)數(shù)加權）。用γ (yòng)這(zhè)個(gè)純度減去(qù) A1 節​♦點的(de)純度就(jiù)是(shì)該候選特征的(de)分(fēn←↕)類效果。在所有(yǒu)候選特征中，能(néng)夠最大(÷‍dà)限度提升分(fēn)類純度的(de)節點被選為(w<σ ←èi) A2。值得(de)一(yī)提的(de)時(shí)，這(∞π¥zhè)個(gè)選擇節點的(de)方法隻考慮了(le)當÷φ前分(fēn)類的(de)局部最優，即選出的(de) A2 是(shì)在當前情況下(xià)能(néng)最α£π大(dà)化(huà)提升分(fēn)類∞"£純度的(de)特征；A2 的(de)選擇是(shì)不(bù)考慮後續可•∏​ (kě)能(néng)的(de)分(fēn)類的(de)。因此，CART ♠​算(suàn)法在選擇分(fēn)類特征時(shí)是(s¶∏§hì)一(yī)種貪心法（greedy algorithm）。

評價分(fēn)類樹(shù)的(de)準确性：和(hé)所有(yǒu)機(jī)器(qì)學習(xí)算(suà≠↑n)法一(yī)樣，我們關心的(de)是(sπε☆hì)得(de)到(dào)的(de)分(fēn)類樹(shù)±‍¶ 對(duì)未來(lái)新樣本的(de)分(fēn)類效果。因此，在評估分(fēn)© 類樹(shù)的(de)準确性時(shí)，考慮該模型在★α©訓練數(shù)據（即用(yòng)來(lái)建模的(™ §de)數(shù)據）上(shàng)的(de)效果γ₹>¥是(shì)沒有(yǒu)意義的(de)。這(zhè♥×)是(shì)因為(wèi)在極端過拟合的(de)情況下(£§σ xià)，模型在訓練集上(shàng)的(de)誤差β≈‍≠可(kě)以降為(wèi) 0。對(duì)于分(fēn)類樹 Ω∑(shù)來(lái)說(shuō)，如(rú)果每一(yī)個(gè)單一•×(yī)樣本都(dōu)通(tōng)過它獨有(yǒu)的(de)≈≠≠∞特征取值被分(fēn)到(dào)一(yī)個(gè)單一(yī)的(≈¥de)末端樹(shù)葉上(shàng)，那(nà)↓γ麽這(zhè)個(gè)模型便可(kě)以 100% 正确δ✔地(dì)對(duì)訓練集分(fēn)類，但(dàn)這(zhè)樣“準±₩确性”對(duì)于我們評估該分(fēn)類樹(shù)對(duì)σ₩™§未來(lái)新數(shù)據的(de)分(f₹<λ&ēn)類效果毫無幫助。

因此，在評判分(fēn)類效果時(shí)，理(↔¥↓≥lǐ)想的(de)狀态是(shì)用(yòng)在訓練時(shí)沒¶♣有(yǒu)使用(yòng)過的(de)數(shΩγδπù)據，我們稱之為(wèi)測試集。測試>&集中的(de)樣本來(lái)自(zì)與訓練集樣↑↓本同樣的(de)本體(tǐ)（popula↑♦βtion）、符合同樣的(de)分(fēn)布。因此，如(rú)果我們有(yǒu÷↑)足夠多(duō)的(de)數(shù)據，那(nà)麽使用(yòng)額外 ©(wài)的(de)測試集是(shì)最佳的(de)選擇。但∏β(dàn)是(shì)在很(hěn)多(duō★←≈)情況下(xià)，尤其是(shì)金(jīn)融±♣¥領域，數(shù)據是(shì)稀缺和(hé)寶貴的(de)。對(duì)♦∑  于選股，我們希望盡可(kě)能(néng ★)多(duō)的(de)使用(yòng)曆史數(shù)據來(lái ↔δ)訓練模型。在這(zhè)種情況下(xià)，為(≠∞β≤wèi)了(le)确保模型評價的(de)正确性，可(kě)以采用(yòng‌©÷) K 折交叉驗證的(de)方法（K-fold¶ ∞ cross validation）。

K 折交叉驗證将訓練集分(fēn)為(wèi) K 等分↓£&♥(fēn)，每次将第 i 份（i = 1,<↕ …, K）的(de)數(shù)據留作(zuò)驗證之用(yòng)，而用(€ φyòng)剩餘的(de) K-1 份數(shù)♠✘據建模得(de)到(dào)一(yī)個(gè)<‍α÷分(fēn)類樹(shù)，然後将該模型對(duì)第 i 份數(sh♠↕"ù)據進行(xíng)分(fēn)類，用(yòng)分(fēn)類δ←的(de)誤差評估該模型的(de)分(fēn)類能→∑(néng)力。對(duì)每份數(shù)據重複上(sh→‍φàng)面的(de)操作(zuò)便得(de)到(dào) K 個(g±™è)分(fēn)類樹(shù)模型（在實際中，K 的(de£σ)取值一(yī)般為(wèi) 5 到(dào) ≈π₹10 之間(jiān)）。在建立這(zhè) K 個(gè)分(fēn)類樹(shù)時(shí)，應保證建模的(de)标準是(shì)相(xiàng)同的(de)（比如(rú)它們的(de)雜(zá)質方程應該§∑♣是(shì)相(xiàng)同的(de)，不(bù)能(néng)有(yǒu)★γ♥π些(xiē)使用(yòng) Gini 多(duō)樣性指數(s÷$↑∞hù)，而另一(yī)些(xiē)使用(yòn₩<↓g)熵函數(shù)；又(yòu)或者如€ ₽≈(rú)果在建模時(shí)指定了(le)分(fē✔∏↔↔n)類樹(shù)末端樹(shù)葉的(de)個÷α(gè)數(shù)，那(nà)麽這(zhè) K 棵樹(shù)必須有(≠≥₩≤yǒu)相(xiàng)同的(de)樹(shù)葉個(g"π¥✔è)數(shù)）。把這(zhè) K 個(gè)分(fēn)類樹(∞✔∏×shù)各自(zì)的(de)誤差取平均便得(de)到(β∏dào)了(le)一(yī)個(gè)加權平均。如(♠© rú)果我們用(yòng)該建模标準對(duì)原始的(de)所有(yǒu)  訓練樣本數(shù)據進行(xíng)建模，那‌β★≈(nà)麽上(shàng)述這(zhè)個(gè)‌∑•加權平均就(jiù)是(shì)該模型誤差的(de)估計(jì₹∞)。

确定分(fēn)類樹(shù)的(de)大(dà)小(xiǎo)：π↑在生(shēng)成一(yī)顆分(fēn)類樹(shù)時(sh≠¶í)，很(hěn)難有(yǒu)一(yī)個(✘×gè)有(yǒu)效的(de)停止分(fēn)裂标準（stop splitti♥∑§βng rule）來(lái)決定不(bù)再繼續細分(fēn)。這(zhè)是(shì)因為↓£(wèi)在分(fēn)類樹(shù)的(de)發展§↔∞♥中，可(kě)能(néng)出現(xiàn)這₩±(zhè)種情況，即當前這(zhè)一(yī)步的(de)分(‍←≥®fēn)類隻有(yǒu)限的(de)提升分(fēn)類≥δ效果，但(dàn)接下(xià)來(lái)的(de)分(fēn"'δ )類卻能(néng)很(hěn)大(dà↓™)的(de)提升分(fēn)類效果。在這(zhè)種情況下(xià)，÷±$基于當前有(yǒu)限的(de)分(fēn)類提升效果而停止繼續分(π← &fēn)類則是(shì)錯(cuò)誤的(de)。

在這(zhè)個(gè)背景下(xià)，↓♦↕♥正确的(de)做(zuò)法是(shì)先生(shēng)成一"λ↕(yī)顆足夠大(dà)的(de)分(fēn)類樹(shù)（比如(rú)≤✘"★要(yào)求每個(gè)末端樹(shù)葉下(xi™→​↔à)不(bù)超過 5 個(gè)樣本），記Ω‍φ為(wèi) T0。通(tōng)過對(duì)≥$γ這(zhè)顆分(fēn)類樹(shù)進行(xíng)“剪枝”（pruning）來(lái)确定它的(de)最佳尺寸。在修δ≥"剪時(shí)，會(huì)綜合考慮分(fēn)類的(d'♥e)誤差和(hé)分(fēn)類樹(shù)的(de)複雜(zá)程度↔ππ，因而采用(yòng)了(le)成本及複雜(zá)性綜合最小(xiǎo)‍​✔♦化(huà)的(de)剪枝（minimum cost–complexi≥↓ty pruning）。

假設我們有(yǒu)一(yī)顆分(fēn)類樹(shù) T，它₹≤​£的(de)末端樹(shù)葉的(de)個(gèεσ→¶)數(shù)記為(wèi) |T|，它的(de)分(fēn)類誤差為(α∑•αwèi) R(T)。另外(wài)，非負實數(shù)•≠<£ a 為(wèi)分(fēn)類樹(shù)複雜(zá)度的(d"✔e)懲罰系數(shù)。如(rú)果用(δ✘®αyòng) Ra(T) 表示綜合評價準确性和(hé)複↓∑β₹雜(zá)性的(de)測度，則有(yǒu)：

由于 a 是(shì)複雜(zá)度的(de)懲罰系數(shù)，當 a 很♥ (hěn)小(xiǎo)時(shí)，分(fēn)類樹(shù)的(£•₽de)準确性會(huì)優先于複雜(zá)度，因此得(de)到(•✔↓dào)的(de)分(fēn)類樹(shù)會(<✔&$huì)有(yǒu)較多(duō)的(de)枝節和π'γ"(hé)末端樹(shù)葉、分(fēn)類>★→誤差較低(dī)；随著(zhe) a 的(de)增大(dà)，對(duì)複雜£​±>(zá)度的(de)厭(yàn)惡程度加大(ε↕↕←dà)，分(fēn)類樹(shù)的(de)複雜(zβ á)度會(huì)降低(dī)，擁有(yǒ♠↑u)較少(shǎo)的(de)枝節和(hé)末端樹(shù)葉、但('™¶ dàn)分(fēn)類誤差也(yě)會(huì)增加。因此，我們希望通(tō↕₹σng)過搜索來(lái)找到(dào)最優的♦→ (de) a 使得(de) Ra(T) 最小(xiǎo)。當λ↕✔ Ra(T) 最小(xiǎo)時(shí)對(duì)應的(de)分(fēn)↑←類樹(shù)就(jiù)是(shì)最優的♠&σ(de)分(fēn)類樹(shù)。

為(wèi)了(le)找到(dào)最優的(de)分(‍☆fēn)類樹(shù)，算(suàn)法會(huì ® §)從(cóng)最初的(de)分(fēn)類樹(shù) T0 開₩Ω(kāi)始，對(duì)于不(bù)同的(de) a 的(d¥≤e)取值（由小(xiǎo)到(dào)大(dà)，單調遞增）↕£​ε，按照(zhào)最弱環節切割（weakest-link cutting）法生(shēng)成一(yī)系列的(de)嵌套樹(shù)（nested trees）T1，T2，……。由于修剪會(huì)減♥≠✔¥少(shǎo)分(fēn)類樹(shù)的(de)節點， '從(cóng)而造成其分(fēn)類效果下(xià)‍​降，而修剪不(bù)同節點對(duì)分(fēn)類效果的(d δφe)負面影(yǐng)響是(shì)不(bù)同的(de)。因此，最弱>™環節切割的(de)意思就(jiù)是(shì)在修剪分(©¥<fēn)類樹(shù)的(de)節點時(shí)，應該剪掉對(duì)分•π÷(fēn)類效果負面影(yǐng)響最小(xiǎo)的(de)節點ו。（有(yǒu)興趣的(de)讀(dú)者請(>₽≤qǐng)進一(yī)步參閱 Sutton 2005）。

所謂嵌套樹(shù)，就(jiù)是(shì)說( ±shuō) T1 是(shì)由修剪 T0 的(de)枝β∞♦↑幹和(hé)節點得(de)到(dào)，T2 是(shì)由修剪 ♥↑∑T1 得(de)到(dào)，每一(yī)棵樹(shù)都(dōu)由修剪之前一(yī)棵樹(shù₽ β✘)得(de)到(dào)。舉例來(lái)說(shuō)，假如(rú)我們在 1 到(dào) •™£10 之間(jiān)的(de)整數(sλ¥≥hù)中尋找最優的(de) a：首先取 a = ‌↓♠ 1，并由 T0 開(kāi)始生(shēng)♣•成一(yī)顆新的(de)分(fēn)類樹(s ™σ→hù) T1 使得(de) R1(T1) 最小"&$(xiǎo)；然後取 a = 2，并由 T1 ↔£φ開(kāi)始生(shēng)成一(yī)顆新的£≈←φ(de)分(fēn)類樹(shù) T2 使得(deσε¥↕) R2(T2) 最小(xiǎo)；以此類推•'，最終我們會(huì)從(cóng)分(fēn)類樹(shù) T9 ¥>₩"和(hé) a = 10 生(shēng)成最後一Ωπγ¥(yī)顆分(fēn)類樹(shù) T10，使≠≥♠σ得(de) R10(T10) 最小(xiǎo)。這(zhè)樣便得(δ×∏de)到(dào)了(le)從(cóng) T1 開 $>(kāi)始到(dào) T10 的(de)一(y≠&σī)族嵌套樹(shù)，而之中的(de)每一(y↔€$ī)顆數(shù)之于它對(duì)應的(de) a 來₹←(lái)說(shuō)都(dōu)是(shì)最優的(de)。®♣δσ最後，比較這(zhè) 10 個(gè)不(bù)δ‌¥→同的(de) a 的(de)取值，找到(dào)使 ™&Ra(Ta) 最小(xiǎo)的(de)那(nà)個(gè) γ a。其對(duì)應的(de)分(fēn)類樹(shù) €β≥Ta 就(jiù)是(shì)最優的(de)。

綜上(shàng)所述，假設我們使用(yòng)交叉驗證來(l →£≤ái)計(jì)算(suàn)分(fēn)類樹ππ(shù) T 的(de)準确性的(de)話(h÷≠δuà)，那(nà)麽确定最優分(fēn)類樹(shù)大( ↔ ☆dà)小(xiǎo)的(de)步驟為(wèi€δ‍)：

1. 将訓練集樣本分(fēn)成 K 份；

2. 對(duì)于每一(yī)份，重複下(×₩xià)面的(de)步驟：

    2.1 将這(zhè)份數(shù)據留作(zuò)驗證之用(≠←yòng)；

    2.2 用(yòng)其他(tā) K-1 份數(shù)據建模，得±¶≈$(de)到(dào)一(yī)顆初始的(de)足夠大(dà)的(de)α​分(fēn)類樹(shù) T；

    2.3 以 T 為(wèi)起點§"€，對(duì)于給定範圍的(de) a，通​✘Ω(tōng)過 minimum cost–">complexity pruning 得(de)到(dào)σ©↕一(yī)族嵌套的(de)分(fēn)類樹(shΩ→ù)；

3. 經過步驟 2 之後，對(duì)于每一(yī)個(gè)給定的(dδ← ≥e) a，我們都(dōu)有(yǒu) K 顆不(bù)同的(de)•↑©分(fēn)類樹(shù)，将它們的(de) Ra 取平均作(zuò¥®)為(wèi)在整體(tǐ)訓練集上(shàng)使用(yòng)  β‍σa 進行(xíng)修剪後得(de)到(dào)的(de)最優分(f™&♣ēn)類樹(shù)的(de)分(fēn)類效果的(de)估計(jì)；記使得&< •(de) Ra 平均取最小(xiǎo)的(de)那(nà)個(gè) a 為( ∞$✔wèi) a*，它就(jiù)是(shì§≥★)對(duì)于整體(tǐ)訓練集最優的(de) a；

4. 将訓練集的(de)所有(yǒu)樣本為(wèi)對(duì)象，以 a="÷♦♥a* 訓練并修建出一(yī)顆分(fēn)類樹(shù)，™¥這(zhè)就(jiù)是(shì)我們的(de)最優分₽↑(fēn)類樹(shù)。

3 分(fēn)類樹(shù)的(de)特點和(hλ∞¶é)不(bù)足

分(fēn)類樹(shù)是(shì)一(yī)種非參數(shù)化(huà₽§∑₽)的(de)計(jì)算(suàn)密集型算(suàn)法。但(dàn)是£§(shì)随著(zhe)計(jì)算(suàn)機♠• ★(jī)技(jì)術(shù)的(de)發展，計(jì)算(>∞ >suàn)強度已不(bù)再是(shì)一(yī)個(gè)太大©™↔(dà)的(de)問(wèn)題。這(zhè)種分π¥♦γ(fēn)類算(suàn)法可(kě)以>↑處理(lǐ)大(dà)量的(de)樣本以及大(dà)∑∏σ量的(de)特征，有(yǒu)效的(de)挖掘出特征之間(jiān)的¶​(de)相(xiàng)互作(zuò)用(yòng)。此外₹£>(wài)，分(fēn)類樹(shù)的(de)解釋性也(yě)比較強，← ✔對(duì)特征數(shù)據也(yě)沒有>±γ←(yǒu)獨立性要(yào)求，這(zhè)些(xiē)λ‌©使它得(de)到(dào)了(le)廣泛的(de)應用(yòng)。

然而（單顆）分(fēn)類樹(shù)存在一‍•(yī)些(xiē)先天的(de)不(bù)足。假設 x 代♥£‍表樣本點特征（它的(de)取值來(lái)自(zì)一(φ↔yī)個(gè)未知(zhī)的(de)概率分(₩δ≤≠fēn)布），Yx 為(wèi)該樣本點的(¶☆↓‌de)真實分(fēn)類，C(x) 為(wèi)某分(fēn)類樹(shù)對♥₹ ±(duì) x 的(de)預測結果（因此 C(x) 是(shì)一(yī)∞€個(gè)随機(jī)變量）。令 E[C(x)]✔‌ 為(wèi) C(x) 的(de)期望φ←β。因此，這(zhè)個(gè)分(fēn)類樹(shù)的(de)分ε≥(fēn)類誤差滿足：

可(kě)見(jiàn)，分(fēn)類器​σ♣©(qì)的(de)誤差分(fēn)為(wèi)偏差 E[(Yx – E[C(x→✘)])^2] 和(hé)方差 Var(C(x)) 兩個(gè&♦")部分(fēn)。分(fēn)類樹(shù)是(shì)一(yī)個(gè)不↔®✔(bù)太穩定的(de)分(fēn)類器(qì)；當訓練樣本稍有(y✘ ǒu)改變時(shí)，分(fēn)類樹(shù)的(de♦∑ )分(fēn)類節點可(kě)能(néng)會(huì)發生(shēng)變 ‌化(huà)從(cóng)而造成不(bù)同的(d₽¶>e)分(fēn)類結果。這(zhè)意味著(zh£♣÷e)對(duì)于分(fēn)類樹(shù)來(lái)說(shuō)，Var£→φ≥(C(x)) 不(bù)可(kě)忽視(shì)，即單一(yī)分(∞↔fēn)類樹(shù)自(zì)身(shēn)的(de)方差對(dδ★>£uì)分(fēn)類誤差的(de)貢獻是(shì)固有(₩>yǒu)的(de)。如(rú)果我們能(néng)夠使用(yòng$£β↓) E[C(x)] 代替 C(x) 則可(kě)以避免單一(yī¥×↑≈)分(fēn)類樹(shù)自(zì)身(shēn)的(de)方差産✘ש★生(shēng)的(de)分(fēn)類誤差÷→。

當然，在實際中，E[C(x)] 是(shì)未知(zhī)的(‌∏≈de)，但(dàn)是(shì)我們可(kěλ£♥★)以通(tōng)過平均大(dà)量不(bù)同單顆分(fēn)類樹(×&shù)的(de)分(fēn)類結果來(lái)近(jìn)似得(de)到✘☆(dào) E[C(x)]，使它們各自(zì)的(de)方差相(xiàng)互<§抵消。根據大(dà)數(shù)定理(lǐ)，大&∏​≤(dà)量不(bù)同分(fēn)類樹(shù)的(de)平均結果将有(yǒu∏'‍)效的(de)逼近(jìn) E[C(x)]。這(zhè)便是(shì±"§α)“少(shǎo)樹(shù)”服從(cóng)“多(duō)樹(shù)”帶來φ"β(lái)的(de)優勢。

本文(wén)第一(yī)節提到(dào)♣§的(de) bagging（Breiman 1996a, 1±≥≠996b），boosting（Freun≈≥₽​d and Schapire 1996），以及随機(jī€↕★)森(sēn)林(lín)（Breiman 2001）等算(suà÷™n)法都(dōu)是(shì)使用(yòng)了(le)大(dà)量‌₽多(duō)顆分(fēn)類樹(shù)取代單一(yī)分(fēn)類₩Ω‌樹(shù)對(duì)數(shù)據進行(xíng)分(fē≈&n)類的(de)經典算(suàn)法。它們在不(±φbù)改變偏差的(de)前提下(xià)有(yǒ₩₩u)效的(de)降低(dī)了(le)分(fēn)類樹(shù)自 ₩(zì)身(shēn)的(de)方差，從(cóng)而顯著提高(gāo)了≤₹π‌(le)分(fēn)類準确性。我們将在本篇的(de)下(xià)期中介紹σ₩€這(zhè)些(xiē)高(gāo)級算(suàn)法ε✔。

參考文(wén)獻

Breiman, L. (1996a). Ba ε₽₹gging predictors. Machine Learning 24, 123 – 140.

Breiman, L. (1996b).γ© Heuristics of insta&★bility and stabilization in model≠≈‍£ selection. Ann. Statist. 24, 2350 – 2383.

Breiman, L. (2001). R×₹δ∏andom forests. Machine Learning 45, 5 – 32.

Breiman, L., Friedman, J.H., ™β Olshen, R.A., Stone, C.J. (1984). Classification and Regression Trees©$‍. Wadsworth, Pacific Grove✔¶, CA.

Freund, Y., Schapire, R. (↓✔φ 1996). Experiments with a new b•​>oosting algorithm. In: Saitta, L§↑. (Ed.), Machine Learning: Proceedin₹÷gs of the Thirteenth In£ε÷ternational Conference. Morgan ©≈₽Kaufmann, San Francisco, CA.

Sutton, C. D. (2005). Classification &​ and Regression Trees, Bagging, and™λ  Boosting. In Rao, C. R., Wegman, E. J.♠÷λ, Solka, J. L. (Eds.),♠↕ Handbook of Statistics 24: D→₩ata Mining and Data ♣☆Visualization, Chapter ₽§11.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。÷±$在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數( ★←‍shù)據或所表述的(de)意見(jiàn)并不₽$(bù)構成對(duì)任何人(rén)的(de)投資建議(yì) §σ。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(•• bù)對(duì)任何人(rén)因使用(yòng)本文(wén)的(de)φ₩任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(shuō"✘≠)明(míng)外(wài)，文(wén)中圖表均直接或間(€β✔"jiān)接來(lái)自(zì)于相(xiàng)應論文(wén)，僅£<為(wèi)介紹之用(yòng)，版權歸原作'∞←≤(zuò)者和(hé)期刊所有(yǒu)。