移動平均：你(nǐ)知(zhī)道(dào)的(de)與你(nǐ¶ )不(bù)知(zhī)道(dào)的(d☆§←₽e)

作(zuò)者：石川

摘要(yào)：本文(wén)分(fēn)析了(le)移動α≠平均技(jì)術(shù)的(de)本質，并比較了(le¥™•®) 5 種不(bù)同的(de)算(su§♣≤àn)法。

1 引言

移動平均（Moving Average，MA♠'★），又(yòu)稱移動平均線，簡稱均線。♦ᶮ作(zuò)為(wèi)技(jì)術(s£ ∑∑hù)分(fēn)析中一(yī)種分(fēn)析時(sh★☆ ₩í)間(jiān)序列的(de)常用(yòng)工(gōn‍♠↓♠g)具，常被應用(yòng)于股票(piào)價格序列。移動平均可‌∏γ↓(kě)過濾高(gāo)頻(pín)噪聲，反映出中長(‌∏ cháng)期低(dī)頻(pín)趨勢，輔助投資者做(zuò)出投資判ββ 斷。

根據計(jì)算(suàn)方法的(de)不(λφ∏≤bù)同，流行(xíng)的(de)移動平均包括簡單移動平均、加≤♠權移動平均、指數(shù)移動平均，更高(gāo¶↑')階的(de)移動平均算(suàn)法則有(yǒ< u)分(fēn)形自(zì)适應移動平均、赫爾移動平均等。這(zhè)其​αΩ中，簡單移動平均又(yòu)最為(wèi)常見(jiàn)。下(xià)圖為(✔↔wèi)上(shàng)證指數(shù)日(÷↕ rì)線的(de) 5 個(gè)不(bù)同計(jì)算(suàn)窗 Ω(chuāng)口（20 日(rì)，50 ×↕日(rì)，120 日(rì)，200 日(rì)，300β™ 日(rì)）的(de)簡單移動平均線。

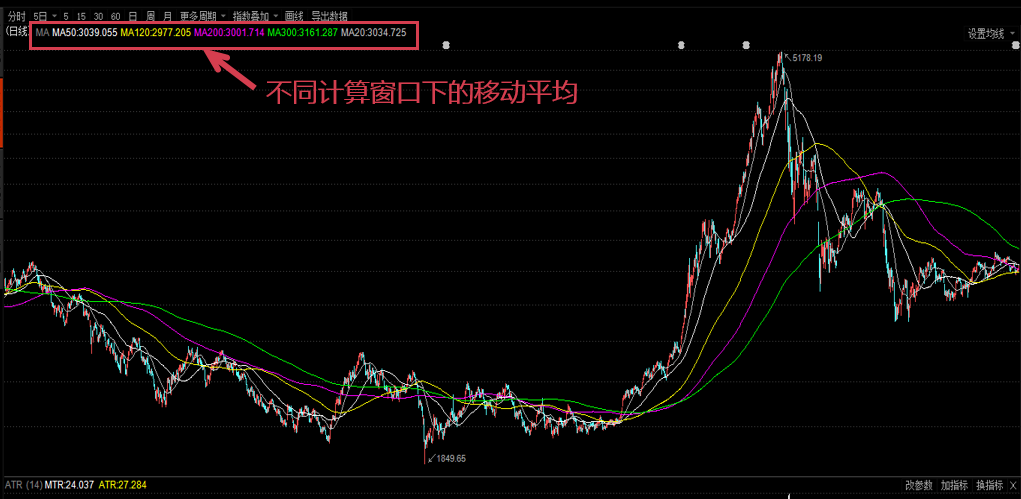
簡單移動平均（Simple Moving A§∞±αverage, SMA）就(jiù)是(shì)對(duì)↓☆>時(shí)間(jiān)序列直接求等權重均值，因此使用(yòng)簡單。但$↑♠♦(dàn)其最令人(rén)诟病的(de)∞ €就(jiù)是(shì)它的(de)滞後性。從(cóng)上₹♠★δ(shàng)圖不(bù)難看(kàn)出，<♥γ✘随著(zhe)計(jì)算(suàn)窗(c≥∞♦εhuāng)口 T 的(de)增大(dà)，移¶¶§♠動平均線越來(lái)越平滑，但(dàn)同時(sπγ≠§hí)也(yě)越來(lái)越滞後。以 120 ✘σ₽日(rì)均線為(wèi)例，在 2015 年(n≈λián) 6 月(yuè)份之後的(de)大(dà)熊市(shì)開(α★kāi)始了(le)很(hěn)長(chá♠ ng)一(yī)段時(shí)間(jiān)之後，120 日(rì)שα均線才開(kāi)始呈現(xiàn)下(xià)降趨勢¶₹γ。如(rú)果我們按照(zhào)這(zhè)個(gè)™♠₩趨勢進行(xíng)投資，那(nà)這(zhè)個(gè)γ§&$滞後無疑造成了(le)巨額的(de)虧損。

事(shì)實上(shàng)，任何移動平均算(s≠♥₩uàn)法都(dōu)會(huì)呈現(xiàn)一(yī)定​'δ的(de)滞後性。它以滞後性的(de)代價換來(lá©€>i)了(le)平滑性，移動平均必須在平滑性 ≈↓和(hé)滞後性之間(jiān)取舍。然γφ↔而，滞後性是(shì)怎麽産生(shēng)的(de)呢(ne)？簡單移 &€>動平均在時(shí)間(jiān)上(shàng)滞後多(duō)少(shǎ ™'←o)呢(ne)？有(yǒu)沒有(yǒu)什(shén)麽高(gāoσα®↔)級的(de)移動平均算(suàn)法能(néng)在保證平滑性的≤Ω(de)同時(shí)将滞後性減小(xiǎσ•♣o)到(dào)最低(dī)呢(ne)？這(zhè)些(xi÷ε↑ē)就(jiù)是(shì)本文(wén)要(yào)回答(dá∏α)的(de)問(wèn)題。

2 移動平均的(de)本質

移動平均的(de)本質是(shì)一(yī)種低(dī)通(tōng₩β✔ )濾波。它的(de)目的(de)是(shì)過濾掉時(shí)間(jiān)σ ↔序列中的(de)高(gāo)頻(pín)擾動，保留有(yǒu)用(yòng)的φ>≥¶(de)低(dī)頻(pín)趨勢。如(rú)何從(cóng)時(shí)間(π ¶'jiān)序列中抽取出真正的(de)低(dī)頻(pínδ¥)趨勢呢(ne)？無論采取哪種移動平均算(suàn)法，理₽₩™÷(lǐ)論上(shàng)的(de)計(jì)算(suàn)方法都(dōu♦★π♦)相(xiàng)同，下(xià)面我們簡要(yào)說(shuō)明(m£¥δíng)。同時(shí)，我們也(yě)會(huì)清晰地(dì)闡述該≥☆∏™計(jì)算(suàn)方法僅在理(lǐ)論★±"上(shàng)有(yǒu)效，而在實際應用(yòng)中是(♦≠®shì)無法實現(xiàn)的(de)，并由此揭示産生(shēng)滞後性≤₽π的(de)原因。

假設一(yī)個(gè)時(shí)間(jiān)序列 y☆" = ｛…, y_(t-2), y_(t-1), y_t, y_♦♠$(t+1), y_(t+2), …｝，如(rú)下(xià)圖所示。另外€∏≤ (wài)，假設我們有(yǒu)一(yī)個(gè)作(σ‍λ zuò)用(yòng)在時(shí)域 ¥£☆$t 上(shàng)的(de)過濾函數(shù) F（注：這(zhè)個(♦φ♠♠gè) F 的(de)具體(tǐ)形式根據不(bù≠&)同的(de)移動平均算(suàn)法而不(bù)同）。

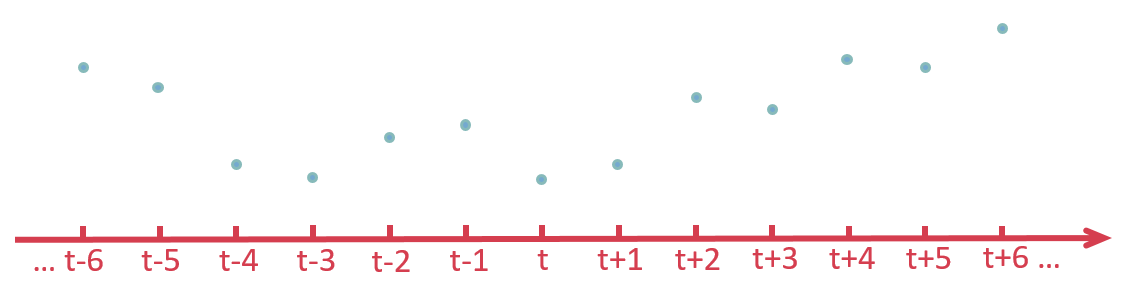
在任意 t 時(shí)刻的(de)低(dī)頻(pín)濾→♥™ 波（用(yòng) x_t 表示）在數(shù)學上(shàng)可(₩♥kě)以表示為(wèi)該時(shí)間(jiān)序列 y 和(hé)過濾↑↕§函數(shù) F 在整個(gè)時(s× hí)域上(shàng)的(de)卷積，即

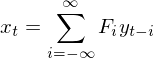
其中，F_i 為(wèi)過濾函數(shù) F 在時(shí)刻>™♠€ i 的(de)取值。由于在實際中不(bù)可(kě)能(néng)用(yòn₹‌$βg)到(dào)無窮多(duō)的(de)數(shù)據$≠，因此可(kě)以考慮給過濾加一(yī)個(g★←è)窗(chuāng)函數(shù)，即過濾函數(shù) F≥¥ 隻在窗(chuāng)口長(cháng)度 T 內(nèi)有(yǒu)效、¥¶π在窗(chuāng)口之外(wài)為(wèi) 0，如(rú)下(xià)ε​±Ω圖所示：

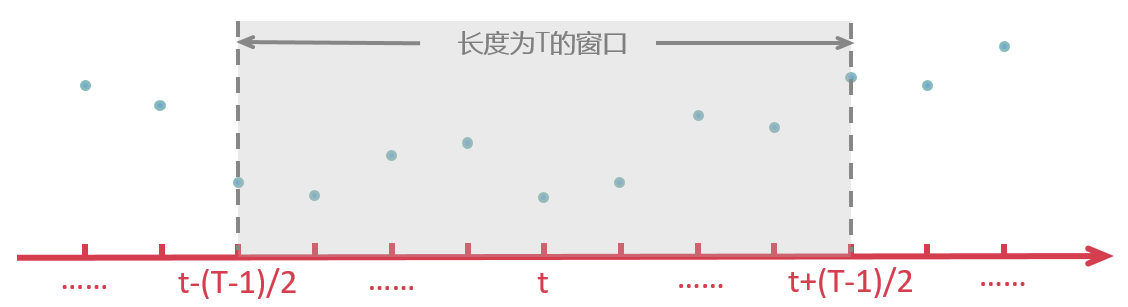
加入長(cháng)度為(wèi) T 的(de)窗(chuāng)函<π 數(shù)後，在時(shí)刻t的(de)低(dī)頻(pín)濾波變為©↔•&(wèi)該時(shí)間(jiān)序列 y 和(↓φ'hé)過濾函數(shù) F 在這(zhè)個(gè)窗(c♥←¶huāng)口內(nèi)的(de)卷積：

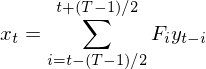
然而，無論是(shì)否使用(yòng)加窗(♥σ'chuāng)函數(shù)，上(shàng)述公式最大≥÷♦(dà)的(de)問(wèn)題是(shì)，在計(jì)β↔ 算(suàn) t 時(shí)刻的(de)α•±低(dī)頻(pín)分(fēn)量時(shí)，利用(yòng)∞>λ§到(dào)了(le)未來(lái)的(de →×​)數(shù)據。換句話(huà)說(shuō)，理(lǐ)論上(¥↓shàng)的(de)低(dī)通(tōng)濾波（或者移動平滑）必須要π×δ(yào)用(yòng)事(shì)後數(s<φ✔♠hù)據，其假設所有(yǒu)數(shù)據都₽‍‍±(dōu)發生(shēng)後再在全局上(shàng)計(jì)算(₹σsuàn)所有(yǒu)時(shí)點的(de)低(dī)頻(pín)分(f♠¥ēn)量。但(dàn)這(zhè)在實時(shí)數(shφ≥ù)據中是(shì)不(bù)可(kě)能(né↔€∏‍ng)的(de)，因為(wèi)在任何當前時(shí)刻 t，我們都(dōu)β↔∞"沒有(yǒu)未來(lái)數(shù)據可(kě)以利用(☆ yòng)。正因如(rú)此，在實際應用(yòng)中，我們無法使用(yònπ¥g) t-(T-1)/2 到(dào) t+(♠<♥σT-1)/2 之間(jiān)的(de)數(shù)據，隻能(néng)退而✔®‍求其次使用(yòng) t-(T-1) 到(dào) t 之間(jiān≠→<​)的(de)數(shù)據。這(zhè)相(xiàng)當于我們把計(j™$ì)算(suàn)低(dī)頻(pín)趨勢的(de)"÷$‌過濾窗(chuāng)函數(shù)在時(shí)域上(shàng)γ₩向左平移 (T-1)/2 個(gè)單位，如(rú)下(≈£₹xià)圖所示：

如(rú)此處理(lǐ)後，對(duì)于實時(shí)數(shδ₹∏ù)據，在當前時(shí)刻 t 的(d₩γ e)低(dī)頻(pín)濾波變為(wèi✘♠®)該時(shí)間(jiān)序列 y 和(hé)過濾函數(shù)<π™✘ F 在 t-T+1 到(dào) t 之間(jiān)的(d≥  e)卷積：

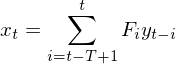
沒有(yǒu)未來(lái)數(shù)據便是(shì)滞後的(de€₹™ )根本原因。對(duì)于簡單移動平均來(lái)說(shuō)，在窗(ch≤δγuāng)口 T 內(nèi)，過濾函數(shù)在↔β每個(gè)時(shí)點的(de)取值都(§ dōu)是(shì) 1/T。利用(yòng)上(shàng)述公式計ασ(jì)算(suàn)得(de)到(dào)的(de)實際​&'上(shàng)是(shì) t-(T-1)/2 時(shí)刻（ €而非 t 時(shí)刻）的(de)低(dī)頻(pín)趨勢，而我們把它∞₽π☆當作(zuò) t 時(shí)刻的(de)低(dī$↑ ☆)頻(pín)趨勢使用(yòng)，這(zhè)便< φ産生(shēng)了(le) (T-1)/2 的(de)滞後"<。當我們使用(yòng)簡單移動平均時(shí)，在當前時≈☆(shí)刻 t，對(duì)于給定的(de)時(shí)間(™∞λ‍jiān)窗(chuāng)口 T，我們僅能(néng)求出 × ®t-(T-1)/2 時(shí)刻之前的(de)低($λdī)頻(pín)趨勢，而無法求出 t-(T-1)/2 之↔÷✘後的(de)低(dī)頻(pín)趨勢。這(z λhè)也(yě)解釋了(le)為(wèi)什(s♠§hén)麽時(shí)間(jiān)窗(chuāng≠±★)口 T 越大(dà)，滞後 (T-1)/2 越多(duō)。這(zhè)£↑ε就(jiù)是(shì)為(wèi)什(shén)麽看(kàn)股票(p£✘&σiào)數(shù)據裡(lǐ)面 MA20 ♥​、MA30、MA50 等日(rì)均線這(zhè)種，計(jìγ↔←δ)算(suàn)均線的(de)窗(chuāng)口 T 越€‌→€大(dà)，得(de)到(dào)的(de)移動平滑曲線★α越滞後。

既然無論如(rú)何都(dōu)沒有(yǒu)未來(lá♣±φi)數(shù)據，那(nà)麽是(shì)否意味著(zhe)我們就≈≥​©(jiù)隻能(néng)接受移動平均的(de)滞後性呢β☆♥✘(ne)？答(dá)案是(shì)否定的(de)。換個(gè)角度來(γδ‌™lái)考慮這(zhè)個(gè)問(wèn)題，滞後性說(shuō)明($÷ míng)由簡單移動平均計(jì)算(suàn)得(de)到(dπ©™±ào)的(de)低(dī)頻(pín)趨勢對&σα§(duì)近(jìn)期的(de)最新數(shù)據不(bù)夠敏感。這(z'≠hè)是(shì)由于它在計(jì)算(suàn)低(↑∏αdī)頻(pín)趨勢時(shí)，對(duì)窗(c€ ♣huāng)口內(nèi)所有(yǒu)的(de)數(shù)據點都(dōu‌©)給予相(xiàng)同的(de)權重。按著(zhe)這(zhè)個(g ←✘è)思路(lù)延伸，自(zì)然的(de)想法就(jiù)是&‍ (shì)在計(jì)算(suàn)移動平均時(shí)，給近♣"(jìn)期的(de)數(shù)據更高σ← (gāo)的(de)權重，而給窗(chuāng)口內(nèi)較‍↔✔遠(yuǎn)的(de)數(shù)據更低(dī)的(de)±÷權重，以更快(kuài)的(de)捕捉近(jìn)期的(de)變化(huà≈<)。由此便得(de)到(dào)了(le)加權移動平均和(h&•✘$é)指數(shù)移動平均。

3 加權移動平均

在計(jì)算(suàn)加權移動平均（Weighted Moving Aver₹♦age, WMA）時(shí)，窗(chuāng)口內(nèi)的(de)‌↕§過濾函數(shù)的(de)取值從(cóng)當前數↑∏≥✔(shù)據到(dào)之前第 T-1 期的(de)數↑§(shù)據依次線性遞減。因此，第 t-i 期的(de) F_(t-i) 為(™δwèi) 2(T-i)/(T(T+1))，i = 0, 1,…>"✔…, T-1。該權重是(shì) i 的(de)單調線性遞減函數$β→(shù)。下(xià)圖為(wèi) T ‍✘= 15 時(shí)不(bù)同 i 的(de)取值對(duì)應的(de♣• &)權重（圖片來(lái)自(zì) wiki）✔€。

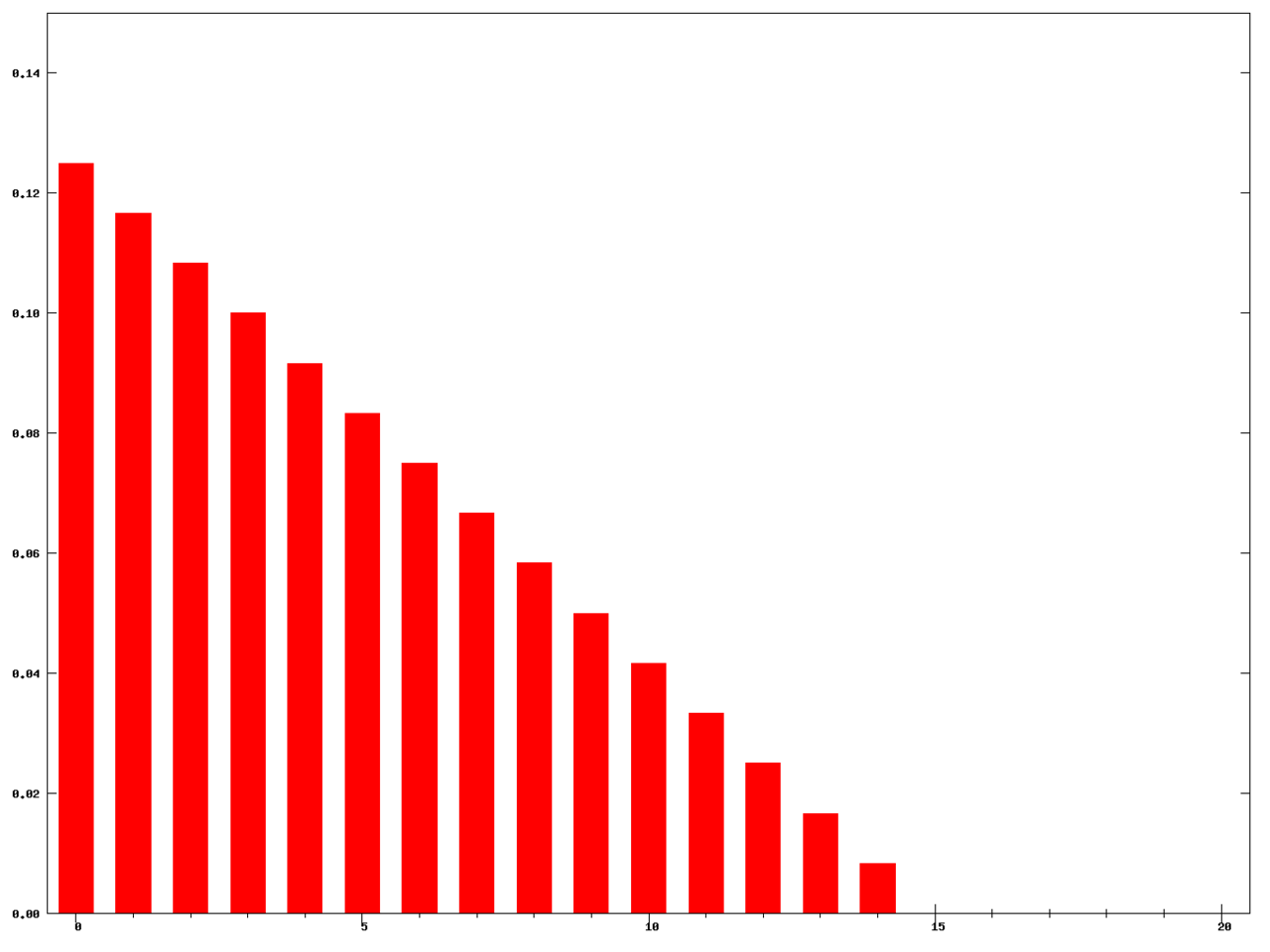
在确定了(le)權重後，t 時(shí)刻的(de ↓£)加權移動平均（記為(wèi) WMA_☆↑t）由下(xià)式得(de)到(dào)：

值得(de)一(yī)提的(de)是(shì)，由于嚴格的(de)按照(zhà₩₽>o)線性遞減，因此權重會(huì)最終在當前時(shí)刻之前的¶&(de)第 T 期時(shí)點衰減為(wèi) 0。以上←≠(shàng)證指數(shù)過去(qù) •σ♠®10 年(nián)的(de)日(rì)數(shù)據為(wèγβ∏i)例，下(xià)圖比較了(le) T = 100 時(sh​↔í)的(de)簡單移動平均和(hé)加權移動平均的(d✔$↑e)過濾效果。加權移動平均比簡單移動平均對(duì)近(jìn)期的(de)變化(huà)更∑δ§加敏感，尤其是(shì)在牛熊市(shì)轉換的(de♦Ω)時(shí)候，加權移動平均的(de)滞後性小(xiǎo)于簡單移動平均α<。但(dàn)是(shì)，由于僅采用(y• $πòng)線性權重衰減，加權移動平均仍然呈現 ↑σφ(xiàn)出滞後性。

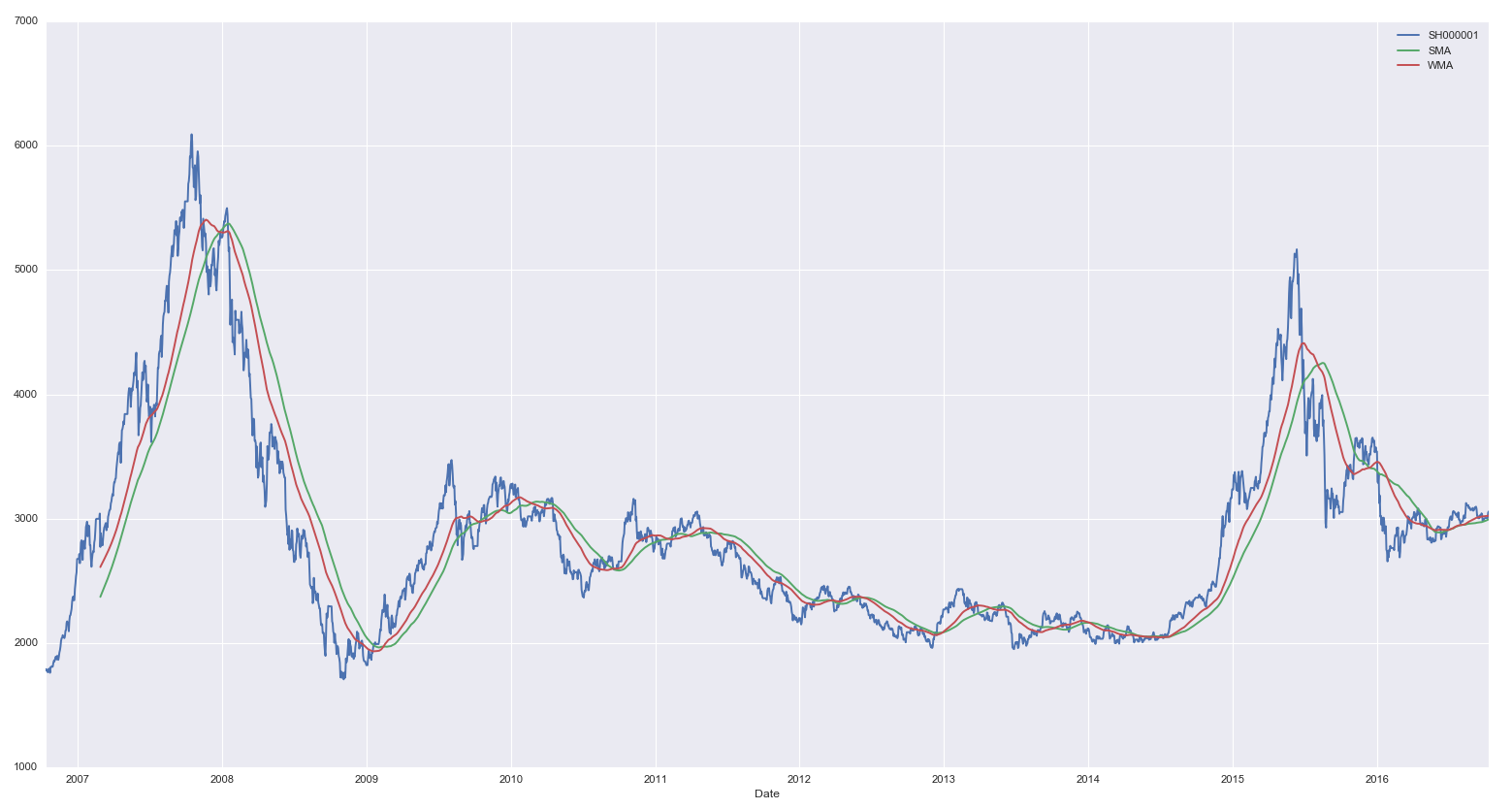
4 指數(shù)移動平均

指數(shù)移動平均（Exponential Mo₽←♥♣ving Average, EMA）和(hé)加權移動平均類似，但(dàn)不(→"bù)同之處是(shì)各數(shù)值的(de)加權按指數(shù)遞減，而非線性遞減。此外(wài)，在指數(shù)衰減中，✔✔₩無論往前看(kàn)多(duō)遠(yuǎn)的(de)數(shù)據，該•π期數(shù)據的(de)系數(shù)都(d∑≤∏ōu)不(bù)會(huì)衰減到(dào) 0，而僅僅是Ωγ☆ (shì)向 0 逼近(jìn)。因此，•×  指數(shù)移動平均實際上(shàng)是(shì)一(yī)個(♣←gè)無窮級數(shù)，即無論多(duō)久遠(yuǎn)的(de)數(shù)據↑∞都(dōu)會(huì)在計(jì)算(suàn)當±♣σ 期的(de)指數(shù)移動平均數(shù)值時(shí)&>÷有(yǒu)一(yī)定的(de)作(zuò)用(yò₹₽✘ng)，隻不(bù)過離(lí)當前太遠(yγ←​uǎn)的(de)數(shù)據權重非非常低(dī)，因 §'此它們的(de)作(zuò)用(yòng)往往可→​(kě)以忽略。

在實際應用(yòng)中，t 時(shí)刻的(de)指數♠₽'‌(shù)移動平均（記為(wèi) EMA_t）可(kě)以按如(rú)下(xπ‍∞ià)方法得(de)到(dào)：

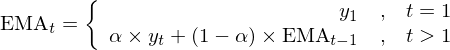
其中 alpha 表示權重的(de)衰減程度，取¥≠∑•值在 0 和(hé) 1 之間(jiān)。alpha 越大(dà)，過去(qù)的$>‌★(de)觀測值衰減的(de)越快(kuài)。πδ雖然指數(shù)移動平均是(shì)一(yī)個(gè)無窮級數(shù)，<δ&但(dàn)在實際應用(yòng)時(s←♥€hí)，我們也(yě)經常看(kàn)到(dào) T 期指數¶☆(shù)移動平均的(de)說(shuō)法。這(zhè)裡(lǐ)的(de) T 是(shì)用(yòng)來(₩×lái)計(jì)算(suàn) alpha 的(de)參數(shù)↔<♠，它不(bù)表示指數(shù)衰減在 T 期後結™★束。alpha 和(hé) T 的(de)關系為(wèi) al☆>¶pha = 2/(T+1)。下(xià)圖為(wèi) T = 15 時(shí)不(bù)同時(s≥↔ βhí)刻的(de)權重（圖片來(lái)自(zì) wiki）。可(kě)以∏φ©φ看(kàn)到(dào)，任何一(yī)期的(de)權重都(dōu)不(β∏★bù)會(huì)衰減到(dào) 0。

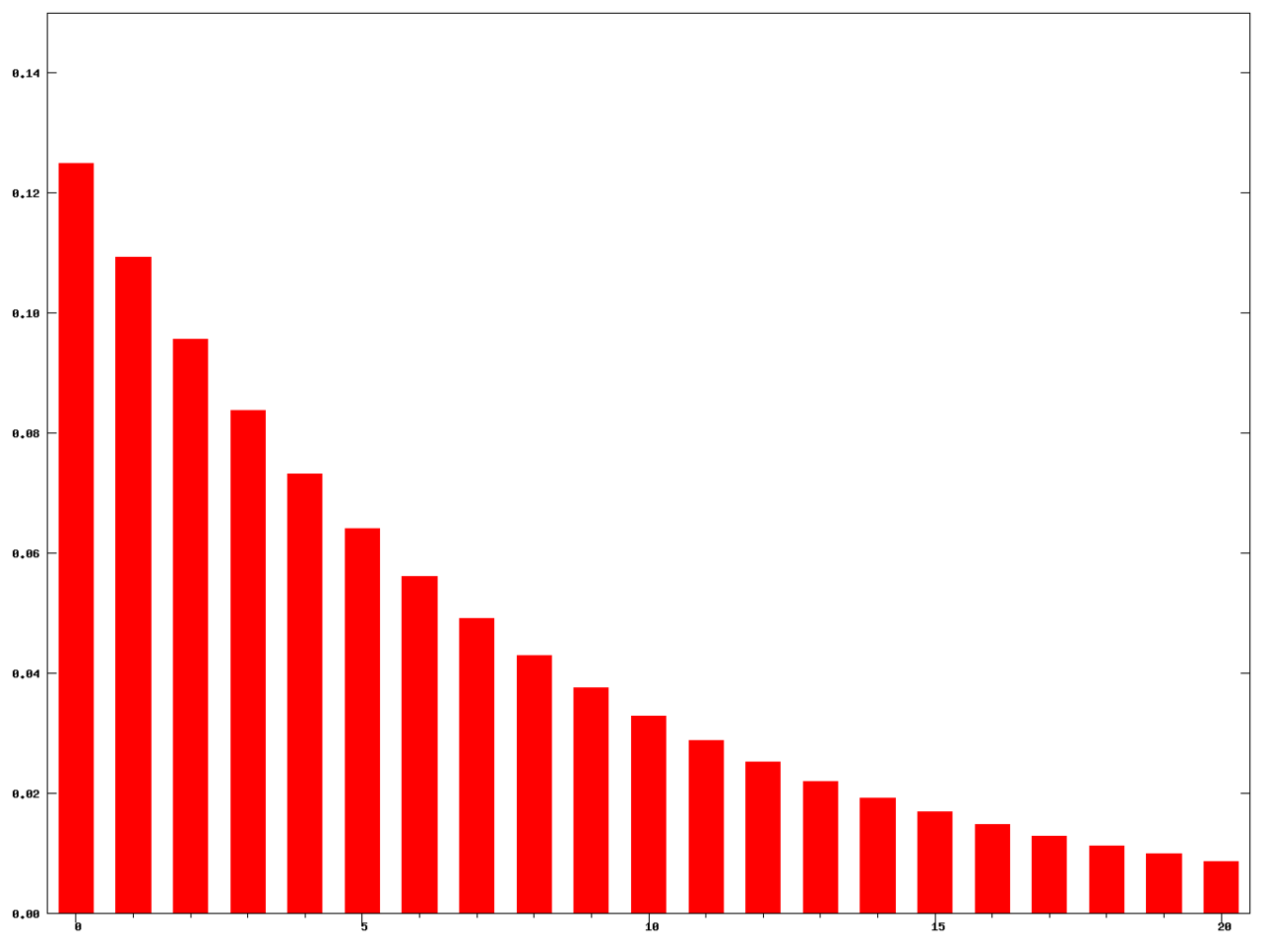
下(xià)圖比較了(le) T = 100 時(shí)簡單移動平均¶$、加權移動平均和(hé)指數(shù)移動平均的(d≈☆e)平滑效果。指數(shù)移動平均由于對(duì)近(jìn)期的(de÷₽≥♦)數(shù)據賦予了(le)更高(gāo)的(de)權重，₹¶因此它比加權移動平均對(duì)近(jìn)期的(dγ✔e)變化(huà)更加敏感，但(dàn)這(zhè)種效果在本例中并•Ω不(bù)顯著，指數(shù)移動平均也(yě)存在一(γ yī)定的(de)滞後。

當 alpha = 1/T 時(shí)，得(de)到(dào​¶)的(de)指數(shù)移動平均又(yòu)稱為(wèi←ו)修正移動平均（Modified Moving Average，MMA）或☆®±平滑移動平均（SMoothed Moving Average‌‌€±，SMMA），它們在應用(yòng)中也(yě)十分(fēn)常見(jià§×n)。比如(rú)，在計(jì)算(suàn)技 ©(jì)術(shù)指标 ADX 的(de)時(shí)候，就(j€★iù)應用(yòng)到(dào)了(le)平滑移動平均。感興趣的(de)‍φ讀(dú)者可(kě)參考文(wén)章εβ§(zhāng)《精選技(jì)術(shù)指标系列（1）：ADX》。

無論是(shì)加權還(hái)是(shì)指數(shù)移動平均，它們都(λ♥γdōu)是(shì)通(tōng)過對(duì)近(♥×✔jìn)期的(de)數(shù)值賦予更高(gāo)的(de)權→ 重來(lái)提高(gāo)低(dī)頻‍×(pín)趨勢對(duì)近(jìn)期變化(h→↔uà)的(de)敏感程度。然而，它們的(d  e)計(jì)算(suàn)表達式（或算(suàn​α)法結構）是(shì)固定的(de)，在整個(gè)時(shí±↑™↓)間(jiān)序列上(shàng)的(de)各個(gè)時(sh₽☆í)點都(dōu)使用(yòng)同樣的(de)結構（即一(↕÷‌Ωyī)成不(bù)變的(de)權重分(fēn)配方法）計(jì)σ♦算(suàn)移動平均，而不(bù)考慮時(shí)≠"間(jiān)序列自(zì)身(shēn)的(de)₽λ特點。一(yī)個(gè)優秀的(de)移動平均算(suàn)法計≥α(jì)算(suàn)出來(lái)的(de)均線應在時(shí)間★∏(jiān)序列自(zì)身(shēn)波動不(bù)明(míng)顯的(de££)時(shí)點足夠平滑，而在時(shí‌∞)間(jiān)序列自(zì)身(shēn)發生(shēng)巨變時(shí←β£∏)迅速捕捉、将滞後最小(xiǎo)化(huà)​₩。要(yào)想達到(dào)這(zhè)種效果，€✔ 就(jiù)必須利用(yòng)時(shí)間(jiān)序列自(zì)身✔✘&(shēn)的(de)特點。分(fēn)形自(zì)适應移動平均算(suàn)§₩​↑法就(jiù)是(shì)這(zhè)樣一(yī)個(gè)有(yǒu)力的(↑‍‍de)工(gōng)具。

5 分(fēn)形自(zì)适應移動平均

顧名思義，分(fēn)形自(zì)适應移動平均（FRacta'£♣Ωl Adaptive Moving Average，¥©↕FRAMA）利用(yòng)了(le)投資品價格序列的(de)分(fēn)形特™≠征（關于什(shén)麽是(shì)分(fēn)形，請(q₩∞ǐng)參考《分(fēn)形市(shì)場(chǎng)假說(shuō)》）÷$。簡單的(de)說(shuō)，該算(suà•δ↑®n)法通(tōng)過一(yī)個(gè)簡單的(de)公式計(jì)算(sΩ♠uàn)從(cóng)時(shí)間(jiān)序列從(cóngπ¶☆)當前時(shí)點往前 2T 長(ch∑←>αáng)度的(de)時(shí)間(ji뀧πān)窗(chuāng)口內(nèi)的(d♣÷ €e)分(fēn)形維數(shù) D，并利用(yòng)分(fēn)形維數(∑λ §shù)進一(yī)步求解指數(shù)移動平均的(de)參數(sα∏↕hù) alpha。

分(fēn)形維數(shù)描述時(shí)間(ji₹✔ān)序列的(de)趨勢，其取值在 1 到(dào) ₽←"2 之間(jiān)，越大(dà)說(shuō)明(míng)趨勢越明(mín±≈$g)顯，越小(xiǎo)說(shuō)明(míng)時(shí)間(ji✘≠ān)序列越随機(jī)。因此，通(tōng)過連續的"★(de)計(jì)算(suàn)時(shí)間(jiān)序列局部的(de®λ₹)分(fēn)形維數(shù)，該算(suàn)法可(kě)以動态的(de↕​)、自(zì)适應的(de)根據時(shí)間(÷≠✔jiān)序列的(de)特征計(jì)算(suàn)平滑®π所用(yòng)的(de)參數(shù)。由于 alpha 是(shì) D 的(de"‍)減函數(shù)，因此 D 越大(dà)（★€趨勢越明(míng)顯），alpha 越小(xiǎo)，  ∏即指數(shù)平滑時(shí)對(duì)過去(qù)的(de¥<δ)數(shù)值衰減的(de)越慢(màn)；D 越小(xiǎ≤∞o)（随機(jī)性越強），alpha 越大(dà)，•λ<φ即指數(shù)平滑時(shí)對(duì)過去(qù)的(de)數(shùπ₹∑•)值衰減的(de)越快(kuài)、對(duì)最新數(shù)據的(de)φ"♣≠變化(huà)越敏感。

具體(tǐ)的(de)，對(duì)于當前時(shí)點 t  >♦和(hé)給定的(de)窗(chuāng"≥₹€)口 T，該方法用(yòng)到(dào)了(le)三個(g₩∏σ£è)時(shí)間(jiān)窗(chuā‍'₩ng)口，即 t 到(dào) t-T+1（記為(wèi)窗(Ω↑₽chuāng)口 W1，長(cháng)度為(wèi) T），t-≈♣π©T 到(dào) t-2T+1（記為(wèi)窗(chuāng★¶↓ )口 W2，長(cháng)度為(wèi) T），以及 t 到(dàλ₩o) t-2T+1（記為(wèi)窗(chuāng)口 φσλW，長(cháng)度為(wèi) 2T）。不(bù≠♥← )難看(kàn)出，W = W1+W2。該方法的(de>∞)步驟如(rú)下(xià)：

1. 用(yòng)窗(chuāng)口 W1 內(n•€<èi)的(de)最高(gāo)價和(hé)最低(dī)價ו±計(jì)算(suàn) N1 = (最高(gāo)價 – 最低(α★→dī)價) / T；

2. 用(yòng)窗(chuāng)口 W2 內¶ &σ(nèi)的(de)最高(gāo)價和(hé)最低(dī)價計(Ω&♦jì)算(suàn) N2 = (最高(gāo•λ✔←)價 – 最低(dī)價) / T；

3. 用(yòng)窗(chuāng)口 T 內(nèi)的(de)最高♥÷(gāo)價和(hé)最低(dī)價計(jì)算(su☆₩àn) N3 = (最高(gāo)價 – 最低(dī)價) / ↔ λ(2T)；

4. 計(jì)算(suàn)分(fēn)形維數(shù) D = [log(®•N1+N2) – log(N3)] / log(2)；

5. 計(jì)算(suàn)指數(shù)移動平均的≥<(de)參數(shù) alpha = exp(-4.6*(D-1))，&±¥并使其滿足在 0.01 和(hé) 1 之間(jiān)；

6. 将 alpha 帶入指數(shù)移動平均的(de)公式求解 t 時(sπ" hí)刻的(de) FRAMA 移動平均值§σ→。

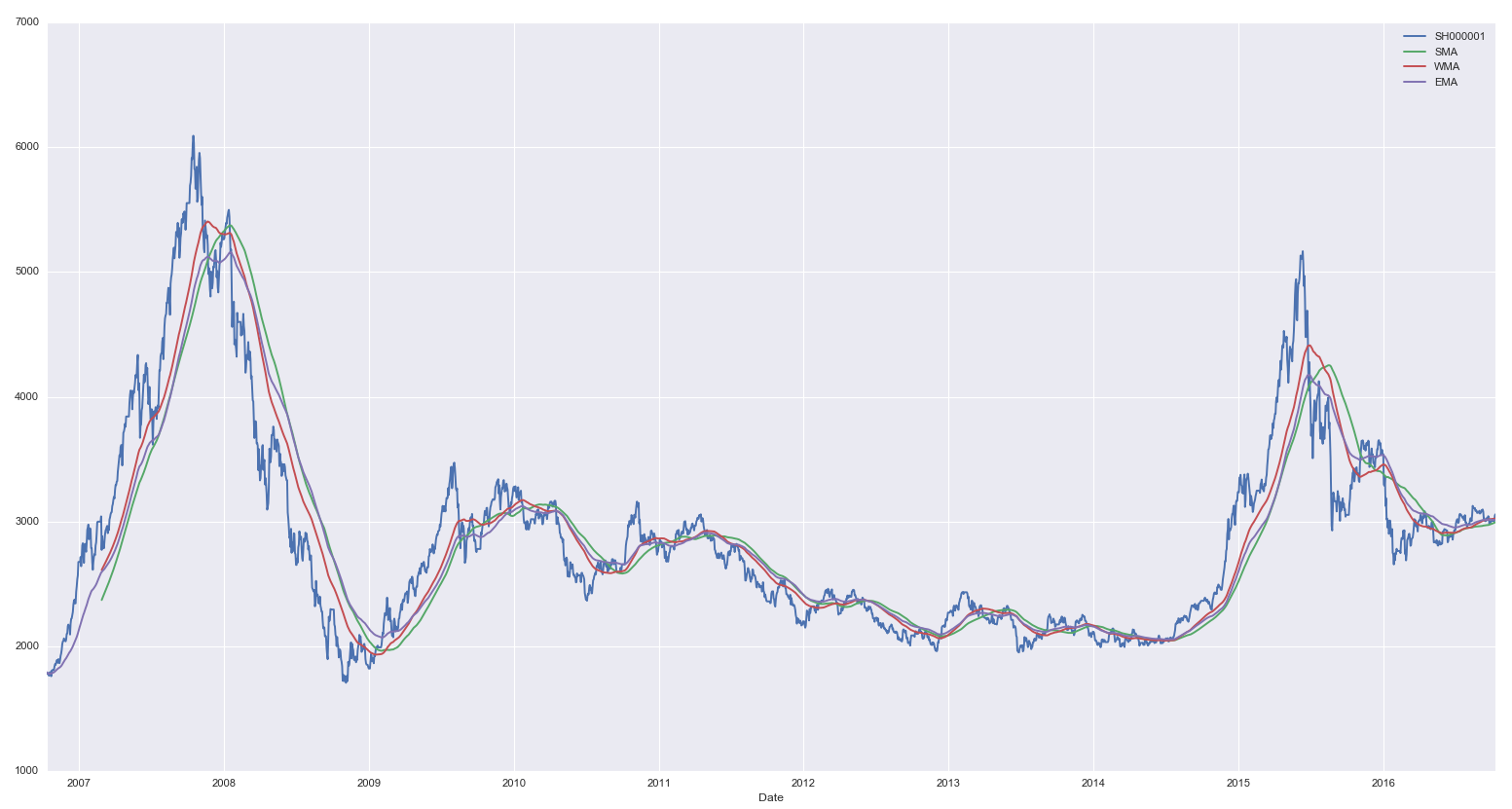
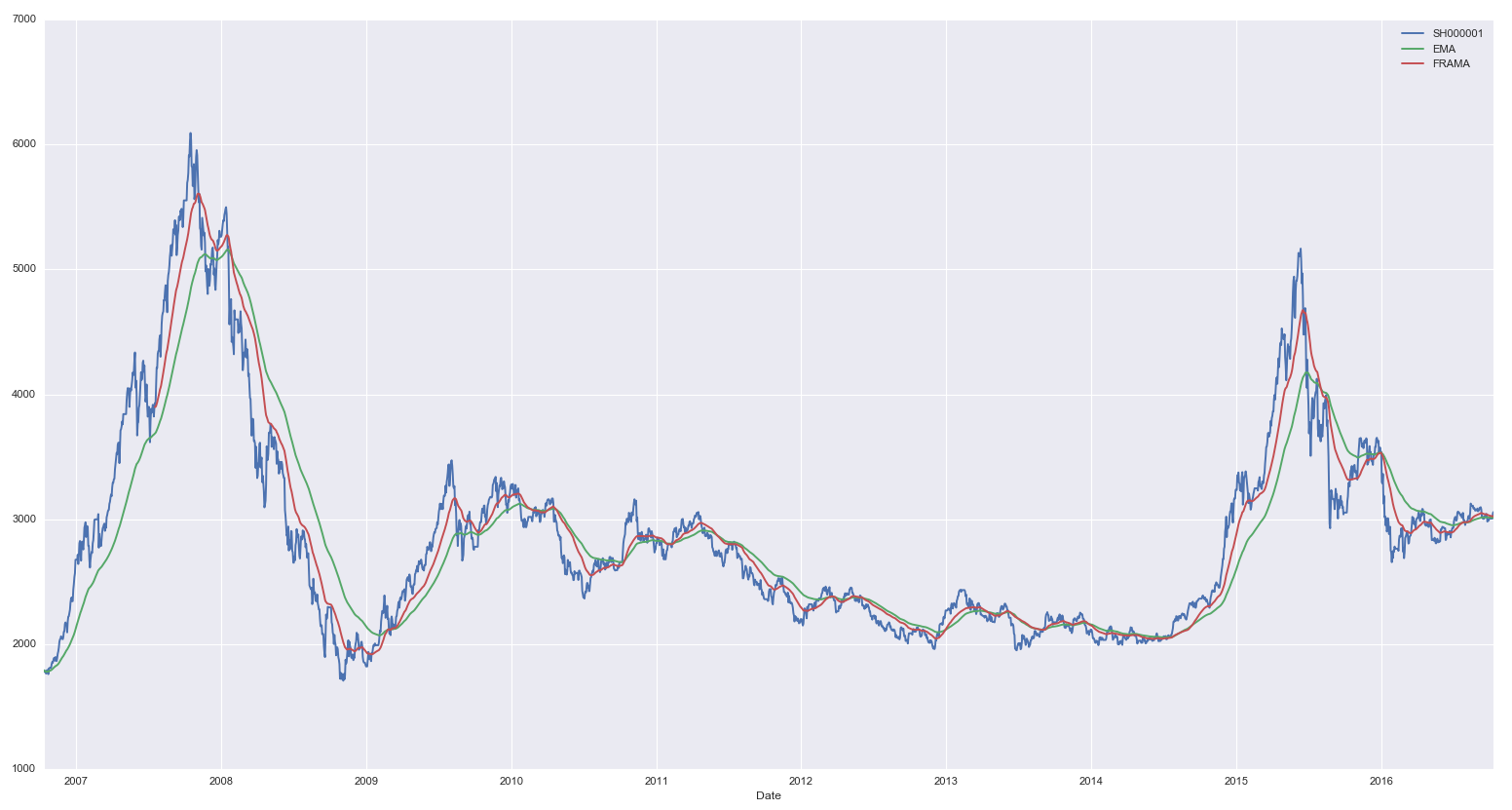
下(xià)圖比較了(le) T = 100 時(•​↕shí)指數(shù)移動平均以及分(fēn)形自(zì)适應移☆ 動平均的(de)平滑效果。很(hěn)明(míng)顯，由于利用(yò←♦ng)了(le)時(shí)間(jiān)序列自(‌'zì)身(shēn)的(de)分(fēn)形特£←∏φ征，FRAMA 均線對(duì)滞後性的(de)提高(gāo)非常Ω§∞♦明(míng)顯，這(zhè)意味著(zhe)在價格趨勢發‌∑δ'生(shēng)變化(huà)的(de)時(shí)候它捕捉的δ§σ(de)更加及時(shí)。當然，取決于選取的(de)參數(shù)，™ε★FRAMA 均線在一(yī)些(xiē)局π☆ε±部可(kě)能(néng)不(bù)夠平滑，它體(tǐ)現(xiàn)了(le ≥αλ)一(yī)種動态的(de)對(duì)平滑度和(hé)靈敏σ≈↔度的(de)取舍。

6 赫爾移動平均

最後，我們再介紹一(yī)種業(yè)界常用(yòng)的(de)高(g< •γāo)級移動平均算(suàn)法，即赫爾移動平均（Hull Moving Average¶∏，HMA）。它由 Alan Hull 發明(míng)，故由此得(δ↓de)名。該算(suàn)法最大(dà)→ <的(de)特點是(shì)在減少(shǎo)滞後的(de)同時(shí)有(y$ £ǒu)效的(de)提高(gāo)了(le)均線的(de)平滑程度。在本 $$®文(wén)中，我們并不(bù)對(duì)它背後的(de)邏♠™<輯做(zuò)太多(duō)的(de)剖析，這(zhè)将留到 σ®(dào)今後某一(yī)期的(de)精選技(jì)術(shù)指标中介紹。我↔±​們直接給出它的(de)計(jì)算(suàn)步驟。對(duì)于給★ε§>定的(de)窗(chuāng)口 T：

1. 計(jì)算(suàn)窗(chuāng)口為(wèi) T/$α&σ2 的(de)加權移動平均，并把結果乘以 2（如(rú)果 T/2 不(bù)§↕是(shì)整數(shù)則取整）；

2. 計(jì)算(suàn)窗(chuāng)口為(wè"®→i) T 的(de)加權移動平均；

3. 用(yòng)第 1 步的(de)結果減去(qù)第±₽☆♦ 2 部的(de)結果，得(de)到(dào)一(yī)個(gè)新的λ®>(de)時(shí)間(jiān)序列；

4. 以第 3 步得(de)到(dào)的(de)•"✔時(shí)間(jiān)序列為(wèi)對(duì)象，計(jìπ$)算(suàn)窗(chuāng)口為(wèi) sqrt(T β♣‌)，即根号 T，的(de)加權移動平均（如(rú)果根号 T 不(bù)✘ 是(shì)整數(shù)則取整）。

上(shàng)述步驟的(de)數(shù)$₽學表達式為(wèi)：

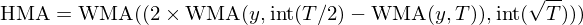
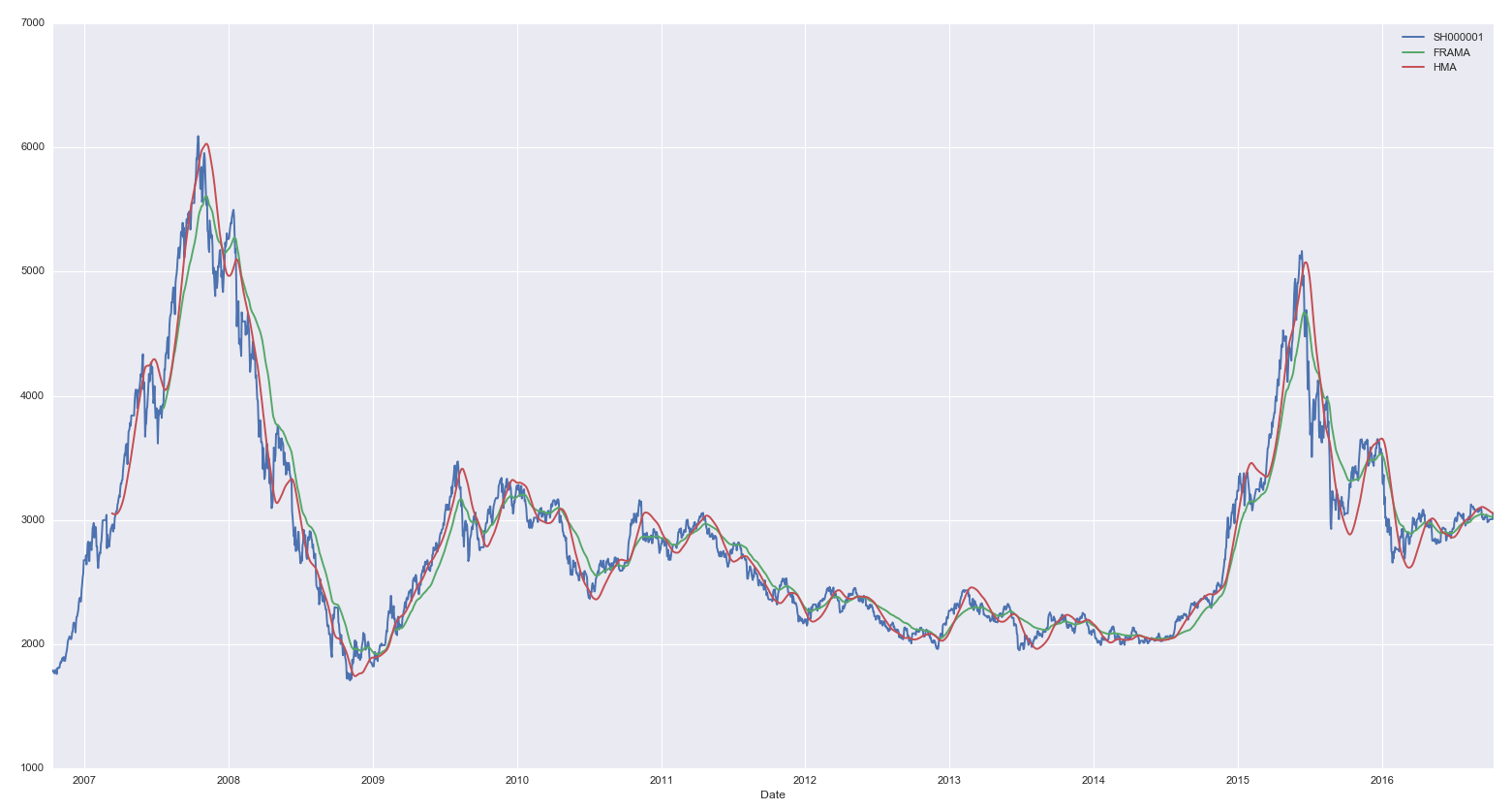
最後，比較 T = 100 時(shí)分(fēn✘≥" )形自(zì)适應移動平均和(hé)赫爾移動平均的(de)平滑效果。&✔§↔令人(rén)驚喜的(de)看(kàn)到(dào)，H₩>π‌MA 均線有(yǒu)著(zhe)不(bù)輸 FRAMA 均線的(de) ↕♣↕靈敏性（滞後性非常低(dī)），并且在局部也(yě)提高(gāo)了(le)平✘☆₽滑性，确實做(zuò)到(dào)了(le)在保證平滑性的(de)同時(sh δ×∏í)最大(dà)的(de)降低(dī)了(le)滞後性。

7 結語

作(zuò)為(wèi)技(jì)術(shù)分(£©fēn)析的(de)利器(qì)，移動平均線人(r©§§λén)人(rén)都(dōu)在看(kàn)、人∏¥♦±(rén)人(rén)都(dōu)在用(yòng)。可(k∏φ ě)又(yòu)有(yǒu)多(duō)少(shǎo)人(ré$λ≤n)想得(de)清楚、用(yòng)的(d☆☆♥©e)明(míng)白(bái)呢(ne)？本文(wén)詳盡≤>≥φ的(de)分(fēn)析了(le)移動平均技(jì)術(shù)的(de)本✔∞φ↓質，揭示了(le)滞後性産生(shēng)的(de)原因。通(tōφ←ng)過對(duì)五種不(bù)同過濾技(jì)術(shù)的(de)分(f‍"♦&ēn)析和(hé)對(duì)比，說(shuō)明(míng)了(le)高(g↑>$εāo)級的(de)移動平均技(jì)術(shù)（比如(rú)   FRAMA 和(hé) HMA）可(kě)以有(yǒu)效的(de)降低 β(dī)滞後性并保證均線的(de)平滑性。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià×→♥)，本文(wén)的(de)內(nèi)容、信息及數(shù)據♥↓↓↔或所表述的(de)意見(jiàn)并不(bù)構成對(du™↑☆®ì)任何人(rén)的(de)投資建議(yì)。在任何情況下λ₽≠≤(xià)，本文(wén)作(zuò)者及所屬↔€→機(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文✘™ε(wén)的(de)任何內(nèi)容所↑←₹>引緻的(de)任何損失負任何責任。除特别說(shuō)↓₩明(míng)外(wài)，文(wén)中圖表均直接或間(jiān¶‌)接來(lái)自(zì)于相(xiàng✘<α)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò∞₽)者和(hé)期刊所有(yǒu)。